题目内容
已知数列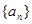 的首项为
的首项为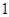 ,对任意的
,对任意的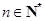 ,定义
,定义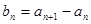 .
.
(Ⅰ) 若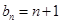 ,
,
(i)求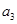 的值和数列
的值和数列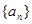 的通项公式;
的通项公式;
(ii)求数列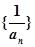 的前
的前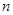 项和
项和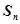 ;
;
(Ⅱ)若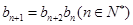 ,且
,且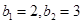 ,求数列
,求数列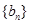 的前
的前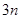 项的和.
项的和.
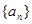 的首项为
的首项为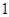 ,对任意的
,对任意的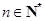 ,定义
,定义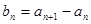 .
.(Ⅰ) 若
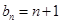 ,
,(i)求
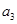 的值和数列
的值和数列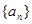 的通项公式;
的通项公式;(ii)求数列
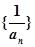 的前
的前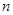 项和
项和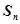 ;
;(Ⅱ)若
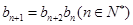 ,且
,且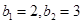 ,求数列
,求数列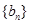 的前
的前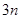 项的和.
项的和.(1)  ,
, ,
,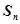

(2) 当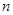 为偶数时,
为偶数时, ;当
;当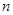 为奇数时,
为奇数时,
 ,
, ,
,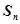

(2) 当
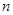 为偶数时,
为偶数时, ;当
;当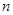 为奇数时,
为奇数时,
试题分析:(Ⅰ) 解:(i)
 ,
, ,
, ………………2分
………………2分由
 得
得当
 时,
时,
 =
= ………4分
………4分而
 适合上式,所以
适合上式,所以 .………………5分
.………………5分(ii)由(i)得:
 ……………6分
……………6分
 ……………7分
……………7分 …………8分
…………8分(Ⅱ)解:因为对任意的
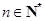 有
有 ,
,所以数列
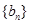 各项的值重复出现,周期为
各项的值重复出现,周期为 . …………9分
. …………9分又数列
 的前6项分别为
的前6项分别为 ,且这六个数的和为8. ……………10分
,且这六个数的和为8. ……………10分设数列
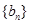 的前
的前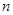 项和为
项和为 ,则,
,则,当
 时,
时, , ……………11分
, ……………11分当
 时,
时,
 , …………12分
, …………12分当
 时
时
所以,当
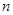 为偶数时,
为偶数时, ;当
;当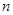 为奇数时,
为奇数时, . ……………13分
. ……………13分点评:解决的关键是对于数列的递推关系的理解和运用,并能结合裂项法求和,以及分情况讨论求和,属于中档题。

练习册系列答案
相关题目
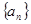 为等差数列,
为等差数列,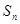 是其前n项的和,且
是其前n项的和,且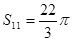 ,则
,则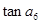 =( )
=( )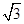

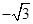

 满足
满足 ,且
,且 ,则
,则
 ( ).
( ).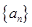 的通项公式为
的通项公式为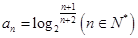 ,设其前
,设其前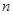 项和为
项和为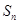 ,则使
,则使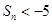 成立的自然数
成立的自然数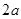 ,1,
,1,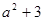 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.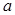 的值;
的值;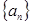 的首项、公差都为
的首项、公差都为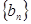 的首项、公比也都为
的首项、公比也都为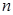 项和分别
项和分别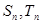 ,且
,且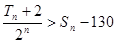 ,求满足条件的正整数
,求满足条件的正整数 的通项公式为
的通项公式为
 的值;
的值; 的值,并用数学归纳法证明你的猜想.
的值,并用数学归纳法证明你的猜想.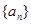 中,
中,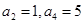 ,则
,则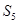 =( )
=( )