题目内容
(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
已知函数 (
( )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 .
.
(1)求 、
、 的值;
的值;
(2)若不等式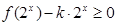 在
在 上有解,求实数
上有解,求实数 的取值范围;
的取值范围;
(3)若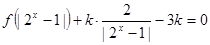 有三个不同的实数解,求实数
有三个不同的实数解,求实数 的取值范围.
的取值范围.
【答案】
(1)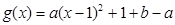 ,……(1分)
,……(1分)
因为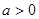 ,所以
,所以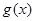 在区间
在区间 上是增函数,故
上是增函数,故 ,解得
,解得 .(3分)
.(3分)
(2)由已知可得 ,……(1分)
,……(1分)
所以 可化为
可化为 ,…………(1分)
,…………(1分)
化为 ,令
,令 ,则
,则 ,因
,因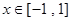 ,故
,故 ,
,
记
 ,因为
,因为 ,故
,故 ,…………(3分)
,…………(3分)
所以 的取值范围是
的取值范围是 .…………(1分)
.…………(1分)
(3)原方程可化为 ,……(1分)
,……(1分)
令 ,则
,则 ,
, 有两个不同的实数解
有两个不同的实数解 ,
, ,其中
,其中 ,
, ,或
,或 ,
,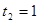 .……(3分)
.……(3分)
记 ,则
,则 ①
①
或 ②
…………(2分)
②
…………(2分)
解不等组①,得 ,而不等式组②无实数解.所以实数
,而不等式组②无实数解.所以实数 的取值范围是
的取值范围是 .
.
………………(2分)
【解析】略

练习册系列答案
相关题目
 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处 中,
中,
 项和
项和 ;
; 项和为
项和为 ,若
,若 对任意
对任意 恒成立,求
恒成立,求 的最小值.
的最小值. 是定义域为R的奇函数.
是定义域为R的奇函数. 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集; 恒成立的
恒成立的 的取值范围;
的取值范围; 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
. ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集; 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 、
、 和
和 的值. 当
的值. 当 对称,且在
对称,且在 处
处