题目内容
设 ,
, 是双曲线
是双曲线 的左右两个焦点,若在双曲线的右支上存在一点
的左右两个焦点,若在双曲线的右支上存在一点 ,使
,使 (
( 为原点)且
为原点)且 ,则双曲线的离心率为( ).
,则双曲线的离心率为( ).
A. | B. | C. | D. |
C
解析试题分析:解:∵ ,∴
,∴ ,
,
∴ ﹣
﹣ =0,OP=OF2=c=OF1,∴PF1⊥PF2,Rt△PF1F2中,∵
=0,OP=OF2=c=OF1,∴PF1⊥PF2,Rt△PF1F2中,∵ ,∴∠PF1F2=30°.由双曲线的定义得 PF1﹣PF2=2a,∴PF2=
,∴∠PF1F2=30°.由双曲线的定义得 PF1﹣PF2=2a,∴PF2= ,sin30°=
,sin30°=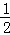 =
= =
= =
= ,∴2a=c(
,∴2a=c( ﹣1),∴
﹣1),∴ =
= +1,
+1,
故选C
考点:双曲线的定义和双曲线的性质
点评:本题考查双曲线的定义和双曲线的简单性质的应用,其中,判断△PF1F2是直角三角形是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
准线方程为x=1的抛物线的标准方程是( )
A. | B. | C. | D. |
过双曲线 左焦点
左焦点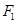 ,倾斜角为
,倾斜角为 的直线交双曲线右支于点
的直线交双曲线右支于点 ,若线段
,若线段 的中点在
的中点在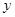 轴上,则此双曲线的离心率为( )
轴上,则此双曲线的离心率为( )
A. | B. | C.3 | D. |
两个顶点在抛物线 上,另一个顶点是此抛物线焦点,这样的正三角形有( )
上,另一个顶点是此抛物线焦点,这样的正三角形有( )
| A.4个 | B.3个 | C.2个 | D.1个 |
以双曲线 的右顶点为焦点的抛物线的标准方程为 ( )
的右顶点为焦点的抛物线的标准方程为 ( )
A. | B. | C. | D. |
已知双曲线 ,其右焦点为
,其右焦点为 ,
, 为其上一点,点
为其上一点,点 满足
满足 =1,
=1,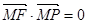 ,则
,则 的最小值为 ( )
的最小值为 ( )
| A.3 | B. | C.2 | D. |
椭圆 的焦距是2,则
的焦距是2,则 =( )
=( )
| A.5 | B.3 | C.5或3 | D.2 |
焦点在x轴上的椭圆 的离心率的最大值为( )
的离心率的最大值为( )
A. | B. | C.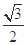 | D. |
若双曲线 (
( ,
, )的一条渐近线被圆
)的一条渐近线被圆 截得的弦长为
截得的弦长为 ,则双曲线的离心率为
,则双曲线的离心率为
A. | B. |
C. | D. |