题目内容
10.函数f(x)=$\sqrt{lg(4-x)}$的定义域为(-∞,3],值域为[0,+∞).分析 根据函数的结构列出限制条件,求解不等式组得到定义域,利用函数设t=lg(4-x),t≥0,y=$\sqrt{t}$求解即可.
解答 解:由题意知$\left\{\begin{array}{l}{lg(4-x)≥0}\\{4-x>0}\end{array}\right.$,
解得:x≤3,
所以函数的定义域为(-∞,3],
∵设t=lg(4-x),t≥0,
∴y=$\sqrt{t}$,
y≥0,
故答案为(-∞,3];[0,+∞).
点评 本题考察函数定义域的求解,属基础题.其中有对数不等式的求解,注意应先将实数化为同底的对数,再利用对数函数的单调性求解

练习册系列答案
相关题目
20.已知函数f(x)=x2-2x+3,当0≤x≤m时,该函数有最大值3,最小值2,则实数m的取值范围是( )
| A. | [1,+∞) | B. | [0,2] | C. | (-∞,2] | D. | [1,2] |
1.执行如图所示的程序框图,则输出i的值为( )
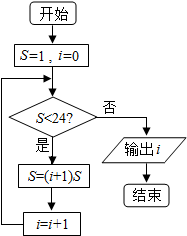

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
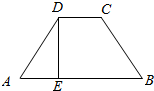 在等腰梯形ABCD中(如图),AB∥CD,DE⊥AB,AB=5,CD=3,∠DAB=$\frac{π}{3}$,现沿DE将等腰梯形折成直二面角.
在等腰梯形ABCD中(如图),AB∥CD,DE⊥AB,AB=5,CD=3,∠DAB=$\frac{π}{3}$,现沿DE将等腰梯形折成直二面角.