题目内容
设命题p:“已知函数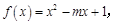 对一切
对一切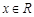 ,
,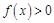 恒成立”,命题q:“不等式
恒成立”,命题q:“不等式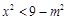 有实数解”,若
有实数解”,若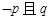 为真命题,则实数m的取值范围为
为真命题,则实数m的取值范围为
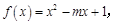 对一切
对一切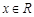 ,
,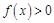 恒成立”,命题q:“不等式
恒成立”,命题q:“不等式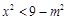 有实数解”,若
有实数解”,若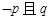 为真命题,则实数m的取值范围为
为真命题,则实数m的取值范围为 [2,3)∪(-3,-2]
解:命题p 为真命题时:x2-mx+1>0在R上恒成立
∴△=m2-4<0 即-2<m<2,
命题q为真命题时:9-m2>0?-3<m<3,
若¬p且q为真命题,则P假且q真.
即 m≤-2 or m≥2
-3<m<3 ?m∈[2,3)∪(-3,-2]
故实数m的取值范围是[2,3)∪(-3,-2].
故答案为:[2,3)∪(-3,-2].
∴△=m2-4<0 即-2<m<2,
命题q为真命题时:9-m2>0?-3<m<3,
若¬p且q为真命题,则P假且q真.
即 m≤-2 or m≥2
-3<m<3 ?m∈[2,3)∪(-3,-2]
故实数m的取值范围是[2,3)∪(-3,-2].
故答案为:[2,3)∪(-3,-2].

练习册系列答案
相关题目
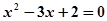 ,则x = 1”的逆否命题为“若x ≠ 1则
,则x = 1”的逆否命题为“若x ≠ 1则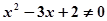 ”;
”; 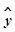 =1+2x中,
=1+2x中, x平均增加1个单位时,
x平均增加1个单位时,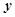 平均增加2个单位 ;
平均增加2个单位 ; 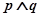 为假命题,则
为假命题,则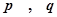 均为假命题 ;
均为假命题 ;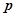 :
: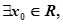 使得
使得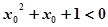 ,则
,则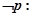
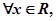 均有
均有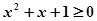 ;
;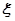 服从正态分布N(0,1),若
服从正态分布N(0,1),若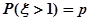 ,则
,则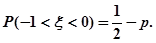
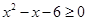 ,命题q:
,命题q: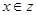 ,若
,若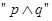 与
与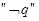 都为假命题,求x的值。
都为假命题,求x的值。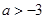 ,则
,则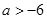 ”以及它的逆命题、否命题、逆否命题中,假命题的个数为( )
”以及它的逆命题、否命题、逆否命题中,假命题的个数为( )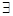 x∈R,使得x2+(a-1)x+1<0”是真命题,则实数a的取值范围是
x∈R,使得x2+(a-1)x+1<0”是真命题,则实数a的取值范围是 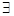 x∈R,使得sinx+cosx=2;
x∈R,使得sinx+cosx=2; x∈(0,π),有sinx>cosx;
x∈(0,π),有sinx>cosx;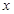 ∈R,使得
∈R,使得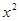 +
+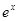 >1+
>1+ ,
,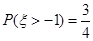 ,
,
 ;
; ”是“直线
”是“直线 与直线
与直线 相互垂直”的充要条件;
相互垂直”的充要条件; 与坐标轴有4个交点,分别为
与坐标轴有4个交点,分别为 ,则
,则 ;
; 的解集为R,则
的解集为R,则
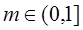 ,则函数
,则函数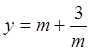 的最小值为
的最小值为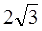 ;
;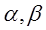 ,直线
,直线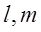 ,若
,若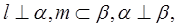 则
则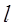 //
//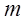 ;
;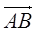 和
和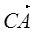 的夹角等于180°-A;
的夹角等于180°-A;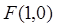 的距离比到直线
的距离比到直线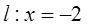 的距离小1,则动点P的轨迹方程为
的距离小1,则动点P的轨迹方程为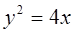 。
。 :“
:“ ”,命题
”,命题 :“直线
:“直线 与圆
与圆 相切”,则
相切”,则