题目内容
方程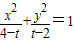 所表示的曲线为C,有下列命题:
所表示的曲线为C,有下列命题:①若曲线C为椭圆,则2<t<4;②若曲线C为双曲线,则t>4或t<2;
③曲线C不可能为圆;④若曲线C表示焦点在y上的双曲线,则t>4;
以上命题正确的是 (填上所有正确命题的序号).
【答案】分析:据椭圆方程的特点列出不等式求出t的范围判断出①错,据双曲线方程的特点列出不等式求出t的范围,判断出②对;据圆方程的特点列出方程求出t的值,判断出③错;据双曲线方程的特点列出不等式求出t的范围,判断出④对.
解答:解:①若C为椭圆应该满足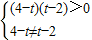 即2<t<4且t≠3,故①错;
即2<t<4且t≠3,故①错;
②若C为双曲线应该满足(4-t)(t-2)<0即t>4或t<2故②对;
③当4-t=t-2即t=3表示圆,故③错;
④若C表示双曲线,且焦点在y轴上应该满足t-2>0,t-4>0则t>4,故④对
综上知②④正确
故答案为②④.
点评:椭圆方程的形式:焦点在x轴时 ,焦点在y轴时
,焦点在y轴时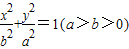 ;双曲线的方程形式:焦点在x轴时
;双曲线的方程形式:焦点在x轴时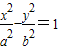 ;焦点在y轴时
;焦点在y轴时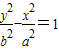
解答:解:①若C为椭圆应该满足
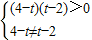 即2<t<4且t≠3,故①错;
即2<t<4且t≠3,故①错;②若C为双曲线应该满足(4-t)(t-2)<0即t>4或t<2故②对;
③当4-t=t-2即t=3表示圆,故③错;
④若C表示双曲线,且焦点在y轴上应该满足t-2>0,t-4>0则t>4,故④对
综上知②④正确
故答案为②④.
点评:椭圆方程的形式:焦点在x轴时
 ,焦点在y轴时
,焦点在y轴时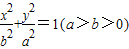 ;双曲线的方程形式:焦点在x轴时
;双曲线的方程形式:焦点在x轴时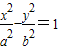 ;焦点在y轴时
;焦点在y轴时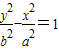

练习册系列答案
相关题目
 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题: ,则C表是长轴在x轴上的椭圆.
,则C表是长轴在x轴上的椭圆. 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题: ,曲线C为椭圆,且焦点坐标为
,曲线C为椭圆,且焦点坐标为 ;
; .
. 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题: ,曲线C为椭圆,且焦点坐标为
,曲线C为椭圆,且焦点坐标为 ;
; .
. 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题: .
.