题目内容
若方程 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:①若C为椭圆,则1<t<4;
②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆;
④若
 ,曲线C为椭圆,且焦点坐标为
,曲线C为椭圆,且焦点坐标为 ;
;⑤若t<1,曲线C为双曲线,且虚半轴长为
 .
.其中真命题的序号为 .(把所有正确命题的序号都填在横线上)
【答案】分析:①若C为椭圆,则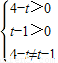 ,故1<t<4且t
,故1<t<4且t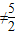 ;
;
②若C为双曲线,则(4-t)(t-1)<0,故t>4或t<1;
③t= 时,曲线C是圆,;
时,曲线C是圆,;
④若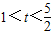 ,曲线C为椭圆,此时焦点在x轴上,由此可得焦点坐标;
,曲线C为椭圆,此时焦点在x轴上,由此可得焦点坐标;
⑤若t<1,曲线C为双曲线,此时焦点在x轴上,由此可得虚半轴长为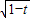 .
.
解答:解:①若C为椭圆,则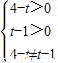 ,∴1<t<4且t
,∴1<t<4且t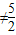 ,故①不正确;
,故①不正确;
②若C为双曲线,则(4-t)(t-1)<0,∴t>4或t<1,故②正确;
③t= 时,曲线C是圆,故③不正确;
时,曲线C是圆,故③不正确;
④若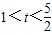 ,曲线C为椭圆,此时焦点在x轴上,且焦点坐标为
,曲线C为椭圆,此时焦点在x轴上,且焦点坐标为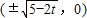 ,故④正确;
,故④正确;
⑤若t<1,曲线C为双曲线,此时焦点在x轴上,且虚半轴长为 ,故⑤正确.
,故⑤正确.
综上真命题的序号为②④⑤
故答案为:②④⑤
点评:本题考查圆锥曲线,考查学生分析解决问题的能力,考查计算能力,属于中档题.
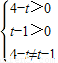 ,故1<t<4且t
,故1<t<4且t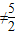 ;
;②若C为双曲线,则(4-t)(t-1)<0,故t>4或t<1;
③t=
 时,曲线C是圆,;
时,曲线C是圆,; ④若
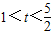 ,曲线C为椭圆,此时焦点在x轴上,由此可得焦点坐标;
,曲线C为椭圆,此时焦点在x轴上,由此可得焦点坐标;⑤若t<1,曲线C为双曲线,此时焦点在x轴上,由此可得虚半轴长为
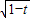 .
.解答:解:①若C为椭圆,则
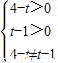 ,∴1<t<4且t
,∴1<t<4且t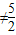 ,故①不正确;
,故①不正确;②若C为双曲线,则(4-t)(t-1)<0,∴t>4或t<1,故②正确;
③t=
 时,曲线C是圆,故③不正确;
时,曲线C是圆,故③不正确; ④若
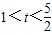 ,曲线C为椭圆,此时焦点在x轴上,且焦点坐标为
,曲线C为椭圆,此时焦点在x轴上,且焦点坐标为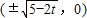 ,故④正确;
,故④正确;⑤若t<1,曲线C为双曲线,此时焦点在x轴上,且虚半轴长为
 ,故⑤正确.
,故⑤正确.综上真命题的序号为②④⑤
故答案为:②④⑤
点评:本题考查圆锥曲线,考查学生分析解决问题的能力,考查计算能力,属于中档题.

练习册系列答案
相关题目
 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题: ,则C表是长轴在x轴上的椭圆.
,则C表是长轴在x轴上的椭圆.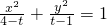 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题: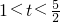 .
. 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题: ,曲线C为椭圆,且焦点坐标为
,曲线C为椭圆,且焦点坐标为 ;
; .
. 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题: .
.