题目内容
12.已知函数f(x)=ax2+bx-2b(1)a=b>0时,解关于x的不等式f(x)<0;
(2)当a=1时,若对任意的x∈(-∞,2),不等式f(x)≥1恒成立,求实数b的取值范围;
(3)若|f(-1)|≤1,|f(1)|≤3,求|a|+|b+2|的取值范围.
分析 (1)当a=b>0时,不等式可化为x2+x-2<0,解之可得;
(2)原不等式化为$b≤\frac{{{x^2}-1}}{2-x},x∈(-∞,2)$恒成立,由基本不等式求右边式子的最小值可得;
(3)可得-1≤a-3b≤1,-3≤a-b≤3,进而可得a∈[-5,5],b∈[-2,2],分类讨论去绝对值可得.
解答 解:(1)当a=b>0时,关于x的不等式f(x)<0可化为bx2+bx-2b<0,
即b(x2+x-2)<0,除以b可得x2+x-2<0,解得-2<x<1
∴f(x)<0的解集为(-2,1);
(2)当a=1时原不等式f(x)≥1可化为b(x-2)≥1-x2,
∵x∈(-∞,2),∴原不等式化为$b≤\frac{{{x^2}-1}}{2-x},x∈(-∞,2)$恒成立,
由基本不等式可得$\frac{{{x^2}-1}}{2-x}=2-x+\frac{3}{2-x}-4≥2\sqrt{3}-4$,
当且仅当2-x=$\frac{3}{2-x}$即x=2-$\sqrt{3}$时取等号,
∴$b≤2\sqrt{3}-4$
(3)由题意题目条件化为-1≤a-3b≤1,-3≤a-b≤3,
作图可知a∈[-5,5],b∈[-2,2],去掉一个绝对值
z=|a|+b+2,对a讨论再去掉一个绝对值.
当-5≤a≤0时,由线性规划得$\frac{5}{3}≤z≤5$;
当0<a≤5时,$\frac{5}{3}<z≤9$,
综上可得$\frac{5}{3}≤z≤9$.
点评 本题考查简单选项规划,涉及基本不等式求最值和恒成立问题,属中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
4.复数z=2-i(i是虚数单位)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,已知锐角α,钝角β的始边都是x轴的非负半轴,终边分别与单位圆交于点P($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),Q(-$\frac{3}{5}$,$\frac{4}{5}$)
如图,已知锐角α,钝角β的始边都是x轴的非负半轴,终边分别与单位圆交于点P($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),Q(-$\frac{3}{5}$,$\frac{4}{5}$)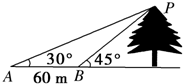 如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.
如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.