题目内容
下列四个命题正确的是
①在频率分布直方图中估计平均数,可以用每个小矩形的高乘以底边的中点的横坐标之和;
②残差平方和越小的模型,拟合的效果越好;
③用相关指数 来刻画回归效果,
来刻画回归效果, 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好;
④随机误差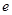 是衡量预报精确度的一个量,它满足
是衡量预报精确度的一个量,它满足 ;
;
⑤对分类变量 和
和 ,它们的随机变量
,它们的随机变量 的观测值
的观测值 来说,
来说, 越小,认为“
越小,认为“ 和
和 有关系”的把握程度越大。
有关系”的把握程度越大。
| A.①③ | B.②④ | C.③⑤ | D.②③ |
B
解析试题分析:根据题意 ,由于①在频率分布直方图中估计平均数,可以用每个小矩形的高乘以底边的中点的横坐标之和;不成立。
②残差平方和越小的模型,拟合的效果越好;成立,
③用相关指数 来刻画回归效果,
来刻画回归效果, 越小,说明模型的拟合效果越好;错误,应该是越大越效果好;④随机误差
越小,说明模型的拟合效果越好;错误,应该是越大越效果好;④随机误差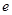 是衡量预报精确度的一个量,它满足
是衡量预报精确度的一个量,它满足 ;成立。
;成立。
⑤对分类变量 和
和 ,它们的随机变量
,它们的随机变量 的观测值
的观测值 来说,
来说, 越小,认为“
越小,认为“ 和
和 有关系”的把握程度越大。错误,应该是越大,故选B
有关系”的把握程度越大。错误,应该是越大,故选B
考点:统计
点评:主要是考查了直方图以及独立性检验的思想的运用,属于基础题。

 快捷英语周周练系列答案
快捷英语周周练系列答案某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名.现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
| A.6 | B.8 | C.10 | D.12 |
某校高三2班有48名学生进行了一场投篮测试,其中男生28人,女生20人.为了了解其投篮成绩,甲、乙两人分别对全班的学生进行编号(1~48号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮考试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:
(Ⅰ)从甲抽取的样本数据中任取两名同学的投篮成绩,记“抽到投篮成绩优秀”的人数为X,求X的分布列和数学期望;
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?
(Ⅲ)判断甲、乙各用何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优?说明理由.
下面的临界值表供参考:
 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 )
) S大学艺术系表演专业的报考人数连创新高,2010年报名刚结束,某考生想知道这次报考该专业的人数.已知该专业考生的考号是按0001,0002,…的顺序从小到大依次排列的,他随机了解了50名考生的考号,经计算,这50个考号的和是25025, 估计2010年报考S大学艺术系表演专业的考生大约有( )
| A.500人 | B.1000人 | C.1500人 | D.2000人 |
某学校有男、女学生各500名.为了解男女学生在学习兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取100名学生进行调查,则宜采用的抽样方法是
| A.抽签法 | B.随机数法 | C.系统抽样法 | D.分层抽样法 |
.以下茎叶图记录了甲.乙两组各五名学生在一次英语听力测试中的成绩(单位:分)
| 甲组 | | 乙组 | |||
| | 9 | 0 | 9 | | |
 | 2 | 1 | 5 |  | 8 |
| 7 | 4 | 2 | 4 | | |
 ,乙组数据的平均数为
,乙组数据的平均数为 ,则
,则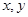 的值分别为 ( )
的值分别为 ( )A.
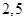 B.
B. C.
C. D.
D.
下图是2013赛季詹姆斯(甲)、安东尼(乙)两名篮球运动员连续参
加的7场比赛得分的 情况,如茎叶图表示,则甲乙两名运动员的中位数分别为( )
| 甲 | | 乙 | ||||
| 5 | 7 | 9 | 1 | 1 | 1 | 3 |
| 3 | 4 | 6 | 2 | 2 | 0 | |
| | | 2 | 3 | 1 | 0 | |
A.23、22 B.19、20 C.26、22 D.23、20
为了评价某个电视栏目的改革效果,在改革前后分别从某居民点抽取了1000位居民进行调查,经过计算得K2 4.358,根据这一数据分析,下列说法正确的是( )
4.358,根据这一数据分析,下列说法正确的是( )
| A.有95%的人认为该栏日优秀 |
| B.有95%的人认为该栏目是否优秀与改革有关系 |
| C.有95%的把握认为电视栏目是否优秀与改革有关系 |
| D.没有理由认为电视栏目是否优秀与改革有关系 |
 个得分去掉
个得分去掉 个最高分,去掉
个最高分,去掉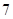 个剩余分数的平均分为
个剩余分数的平均分为 ,现场做的
,现场做的 表示:
表示: