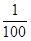题目内容
某校高三2班有48名学生进行了一场投篮测试,其中男生28人,女生20人.为了了解其投篮成绩,甲、乙两人分别对全班的学生进行编号(1~48号),并以不同的方法进行数据抽样,其中一人用的是系统抽样,另一人用的是分层抽样.若此次投篮考试的成绩大于或等于80分视为优秀,小于80分视为不优秀,以下是甲、乙两人分别抽取的样本数据:
(Ⅰ)从甲抽取的样本数据中任取两名同学的投篮成绩,记“抽到投篮成绩优秀”的人数为X,求X的分布列和数学期望;
(Ⅱ)请你根据乙抽取的样本数据完成下列2×2列联表,判断是否有95%以上的把握认为投篮成绩和性别有关?
(Ⅲ)判断甲、乙各用何种抽样方法,并根据(Ⅱ)的结论判断哪种抽样方法更优?说明理由.
下面的临界值表供参考:
 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 )
)
(Ⅰ) 的分布列为
的分布列为






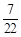
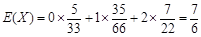 .
.
(Ⅱ)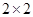 列联表:
列联表:
有95%以上的把握认为投篮成绩与性别有关. 优秀 非优秀 合计 男[来源:学+科+网Z+X+X+K] 6 1 7 女 1 4 5 合计 7 5 12
(Ⅲ)甲用的是系统抽样,乙用的是分层抽样.投篮成绩与性别有关,并且从样本数据能看出投篮成绩与性别有明显差异,因此采用分层抽样方法比系统抽样方法更优.
解析试题分析:(Ⅰ)由“抽到投篮成绩优秀”的人数为X,其所有可能取值为 以下茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩(单位:分),已知甲组数据的中位数为15,乙组数据的平均数为16.8,则 有20位同学,编号从1至20,现在从中抽取4人作问卷调查,用系统抽样方法确定所抽的编号为( ) 废品率 甲、乙两棉农,统计连续五年的面积产量(千克∕亩)如下表: 下列四个命题正确的是 一名小学生的年龄和身高(单位:cm)的数据如下: .
.
计算可得相应概率,得到 的分布列为
的分布列为






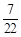
计算得到数学期望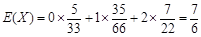 .
.
(Ⅱ)由乙抽取的样本数据,得到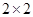 列联表,应用“卡方公式”计算“卡方”并与临界值表对照,得出结论.
列联表,应用“卡方公式”计算“卡方”并与临界值表对照,得出结论.
(Ⅲ)对照系统抽样、分层抽样的定义.确定抽样方法,由(Ⅱ)的结论,并且从样本数据能看出投篮成绩与性别有明显差异,得到结论.
试题解析:(Ⅰ)由甲抽取的样本数据可知,投篮成绩优秀的有7人,投篮成绩不优秀的有5人.
X的所有可能取值为 . 1分
. 1分
所以 ,
, ,
, .4分
.4分
故 的分布列为
的分布列为
5分






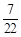
∴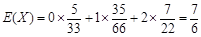 . 6分
. 6分
(Ⅱ)设投篮成绩与性别无关,由乙抽取的样本数据,得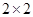 列联表如下:
列联表如下: 优秀 
中考全程总复习系列答案
阅读课堂北京教育出版社系列答案
1日1练口算题卡系列答案


培优新题库系列答案
教材备考笔记系列答案
竖式计算卡系列答案

名校直通车系列答案
 的值分别为( )
的值分别为( )
A.5,2 B.5,5 C.8,5 D.8,8 A.5,10,15,20 B.2,6,10,14 C.2,4,6,8 D.5,8,11,14  和每吨生铁成本
和每吨生铁成本 (元)之间的回归直线方程为
(元)之间的回归直线方程为 ,这表明 ( )
,这表明 ( )A.  与
与 的相关系数为2
的相关系数为2B.  与
与 的关系是函数关系的充要条件是相关系数为1
的关系是函数关系的充要条件是相关系数为1C.废品率每增加1%,生铁成本增加258元 D.废品率每增加1%,生铁成本平均每吨增加2元
则平均产量较高与产量较稳定的分别是棉农甲
68
72
70
69
71
棉农乙
69
71
68
68
69
A.棉农甲,棉农甲 B.棉农甲,棉农乙
C.棉农乙,棉农甲 D.棉农乙,棉农乙
①在频率分布直方图中估计平均数,可以用每个小矩形的高乘以底边的中点的横坐标之和;
②残差平方和越小的模型,拟合的效果越好;
③用相关指数 来刻画回归效果,
来刻画回归效果, 越小,说明模型的拟合效果越好;
越小,说明模型的拟合效果越好;
④随机误差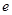 是衡量预报精确度的一个量,它满足
是衡量预报精确度的一个量,它满足 ;
;
⑤对分类变量 和
和 ,它们的随机变量
,它们的随机变量 的观测值
的观测值 来说,
来说, 越小,认为“
越小,认为“ 和
和 有关系”的把握程度越大。
有关系”的把握程度越大。A.①③ B.②④ C.③⑤ D.②③
由散点图可知,身高y与年龄x之间的线性回归直线方程为年龄X 6 7 8 9 身高Y 118 126 136 144  ,预测该学生10岁时的身高为( )
,预测该学生10岁时的身高为( )
A. 154 B. 153 C. 152 D. 151


 人,其中高三年级学生数是高一年级学生数的两倍,高二年级学生比高一年级学生多
人,其中高三年级学生数是高一年级学生数的两倍,高二年级学生比高一年级学生多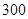 人,现按年级用分层抽样的方法从高一年级、高二年级、高三年级抽取一个学生样本. 如果在这个样本中,有高三年级学生
人,现按年级用分层抽样的方法从高一年级、高二年级、高三年级抽取一个学生样本. 如果在这个样本中,有高三年级学生 人,那么为得到这个样本,在从高二年级抽取学生时,高二年级每个学生被取到的概率为( )
人,那么为得到这个样本,在从高二年级抽取学生时,高二年级每个学生被取到的概率为( )