题目内容
如下图,四面体ABCD中,E、F分别是AC、BD的中点,若CD=2AB=2,EF⊥AB,则EF与CD所成的角等于___________.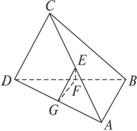
答案:30°
解析:取AD的中点G，连结EG、FG，易知EG=1，FG=
.
由EF⊥AB及GF∥AB知EF⊥FG.
在Rt△EFG中，求得∠GEF=30°，即为EF与CD所成的角.
练习册系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
学练快车道快乐假期寒假作业系列答案题目内容
如下图,四面体ABCD中,E、F分别是AC、BD的中点,若CD=2AB=2,EF⊥AB,则EF与CD所成的角等于___________.
答案:30°
解析:取AD的中点G，连结EG、FG，易知EG=1，FG=.
由EF⊥AB及GF∥AB知EF⊥FG.
在Rt△EFG中，求得∠GEF=30°，即为EF与CD所成的角.
学练快车道快乐假期寒假作业系列答案
，AC＝BC，△ABD中，∠ABD＝
，∠D＝
．设AC＝a．现将四边形ACBD沿着AB翻折成直二面角C－AB－D，连结CD得一个四面体(如下图)．
．F是线段PB上一点，
，点E在线段AB上，且EF⊥PB．
=a,
=b,
=c,D为BC中点,E为AD的中点,则
=_____.(用a,b,c表示)