题目内容
如下图(1),四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,如下图(2),则在四面体ABCD中,下列命题正确的是( )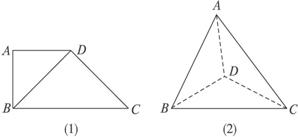
A.平面ABD⊥平面ABC B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC D.平面ADC⊥平面ABC
答案:D
解析:翻折前,由已知可得∠DBC=∠DCB=45°,
∴∠BDC=90°,即BD⊥DC.
翻折后,由平面ABD⊥平面BCD,可得CD⊥面ABD.
∴CD⊥AB.又AB⊥AD,
∴AB⊥面ADC.而AB![]() 面ABC,
面ABC,
∴面ABC⊥面ADC.选项D正确.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
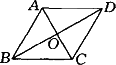

 π,∠AOP=120°。
π,∠AOP=120°。
