题目内容
将一副三角板放在同一个平面上组成下图所示的四边形ACBD,△ABC中,∠C=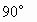 ,AC=BC,△ABD中,∠ABD=
,AC=BC,△ABD中,∠ABD=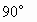 ,∠D=
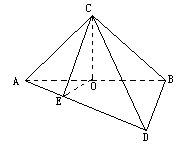
,∠D=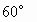 .设AC=a.现将四边形ACBD沿着AB翻折成直二面角C-AB-D,连结CD得一个四面体(如下图).
.设AC=a.现将四边形ACBD沿着AB翻折成直二面角C-AB-D,连结CD得一个四面体(如下图).
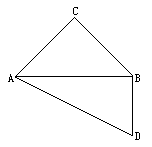
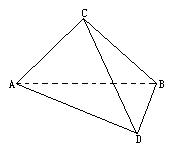
(1)求证:平面ACD⊥平面BCD;
(2)求直线AD和BC所成的角;
(3)求直线AD和平面BCD所成的角;
(4)求平面ACD和平面ABD所成二面角的大小.
解析:
|
证明(1)∵∠ABD= ∵C-AB-D是直二面角,∴DB⊥平面ABC. ∴AC⊥BD. 又∵∠ACB= ∴AC⊥平面BCD. ∴平面ACD⊥平面BCD. 解(2)作AE∥DB,取AE=DB(如图).则ADBE是平行四边形.BE∥DA,BC与BE所成的锐角即是异面直线AD与BC所成的角.设AB与DE相交于O,则O是AB和DE的中点,∴CO⊥AB.∵C-AB-D是直二面角,∴CO⊥平面ADBE.∵OD=OE,∴CE=CD,而
解(3)由(1)已证DB⊥平面ABC,∴AC⊥BD.又AC⊥BC,∴AC⊥平面BCD且AC⊥CD.于是∠CDA为AD与平面BCD所成的角.在Rt△ACD中,AC=a,
解(4)过C作CO⊥AB,O为垂足. ∵平面ABC⊥平面ABD,∴CO⊥平面ABD.在平面ABD内,作OE⊥AD,E为垂足,连结CE.根据三垂线定理,有CE⊥AD,∠CEO就是所求二面角的平面角. ∵AC=a,AC=BC,∠ACB= ∴AO=BO=CO= ∵∠ABD= 在Rt△COE中,
|
提示:
|
本题也可以用中位线法得出两条异面直线所成的角,然后计算出二面角的平面角的大小.如图,M,N,O分别是AC,CD,AB的中点,则MN与OM所成的锐角就是异面直线AD与BC所成的角.在直角△COD中,ON是斜边上的中线,得
|

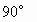 ,∴DB⊥AB.
,∴DB⊥AB.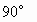 ,∴AC⊥BC.
,∴AC⊥BC.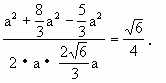 ∴∠CBE=
∴∠CBE=
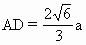 ,∴
,∴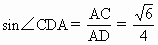 ,∠CDA=
,∠CDA= 即为所求AD与平面BCD所成的角.
即为所求AD与平面BCD所成的角.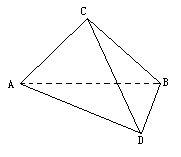
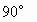 ,CO⊥AB,
,CO⊥AB,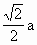 .
.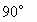 ,∠ADB=
,∠ADB= ,∴
,∴ .
.
 .不难计算得出结果.
.不难计算得出结果.
 如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6.
如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6. 如图,将一副三角板拼成直二面角A-BC-D,其中∠BAC=90°,AB=AC,∠BCD=90°,∠CBD=30°.
如图,将一副三角板拼成直二面角A-BC-D,其中∠BAC=90°,AB=AC,∠BCD=90°,∠CBD=30°. 如图,将一副三角板拼接,使它们有公共边BC,若使两个三角形所在的平面互相垂直,且∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6.
如图,将一副三角板拼接,使它们有公共边BC,若使两个三角形所在的平面互相垂直,且∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6. 如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6.
如图所示,将一副三角板拼接,使它们有公共边BC,且使两个三角形所在的平面互相垂直,若∠BAC=90°,AB=AC,∠CBD=90°,∠BDC=60°,BC=6.