题目内容
2.三棱锥P-ABC内接于球O,球O的表面积是24π,∠BAC=$\frac{π}{3}$,BC=4,则三棱锥P-ABC的最大体积是$\frac{16\sqrt{2}}{3}$.分析 设球的半径为R,球心为O,如图所示,由球O的表面积是24π,可得4πR2=24π,解得R.设△ABC的外心为O1,外接圆的半径为r,则O1B=r=$\frac{1}{2}×$$\frac{4}{sin\frac{π}{3}}$,可得$O{O}_{1}=\sqrt{O{B}^{2}-{O}_{1}{B}^{2}}$.可得O1P=$\sqrt{6}+\frac{\sqrt{6}}{3}$.在△ABC中,由余弦定理可得:${4}^{2}={b}^{2}+{c}^{2}-2bccos\frac{π}{3}$,利用基本不等式的性质可得bc≤16,利用三棱锥P-ABC的体积V=$\frac{1}{3}×{S}_{△ABC}×{O}_{1}P$,即可得出.
解答 解:设球的半径为R,球心为O,如图所示,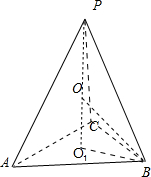
∵球O的表面积是24π,∴4πR2=24π,解得$R=\sqrt{6}$.
设△ABC的外心为O1,外接圆的半径为r,则O1B=r=$\frac{1}{2}×$$\frac{4}{sin\frac{π}{3}}$=$\frac{4}{\sqrt{3}}$,
∴$O{O}_{1}=\sqrt{O{B}^{2}-{O}_{1}{B}^{2}}$=$\frac{\sqrt{6}}{3}$.
∴O1P=$\sqrt{6}+\frac{\sqrt{6}}{3}$=$\frac{4\sqrt{6}}{3}$.
在△ABC中,由余弦定理可得:${4}^{2}={b}^{2}+{c}^{2}-2bccos\frac{π}{3}$,
化为b2+c2=bc+16≥2bc,∴bc≤16,当且仅当b=c=4时取等号.
∴三棱锥P-ABC的体积V=$\frac{1}{3}×{S}_{△ABC}×{O}_{1}P$=$\frac{1}{3}×\frac{1}{2}bcsin\frac{π}{3}$×$\frac{4\sqrt{6}}{3}$≤$\frac{2\sqrt{6}}{9}×\frac{\sqrt{3}}{2}×16$=$\frac{16\sqrt{2}}{3}$,
故答案为:$\frac{16\sqrt{2}}{3}$.
点评 本题考查了三棱锥外接球的性质、勾股定理、三棱锥的体积计算公式、正弦定理余弦定理、基本不等式的性质,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | (0,+∞) | B. | [0,+∞) | C. | (-∞,0) | D. | (-1,+∞) |
 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,G和H分别是CE和CF的中点.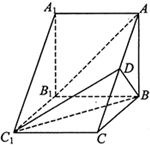 在三棱柱ABC-A1B1C1中,侧棱BB1⊥底面A1B1C1,D为AC 的中点,A1B1=BB1=2,A1C1=BC1,∠A1C1B=60°.
在三棱柱ABC-A1B1C1中,侧棱BB1⊥底面A1B1C1,D为AC 的中点,A1B1=BB1=2,A1C1=BC1,∠A1C1B=60°. 如图,边长为2的正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面,且AE=1
如图,边长为2的正方形ABCD所在平面与圆O所在平面相交于CD,CE为圆O的直径,线段CD为圆O的弦,AE垂直于圆O所在平面,且AE=1