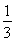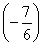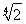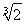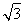Question

已知函数f(x)＝2x－，x∈(0，1]．

(1)当a＝－1时，求函数y＝f(x)的值域；

(2)若函数y＝f(x)在x∈(0，1]上是减函数，求实数a的取值范围．

 

Answer 1

（1）[2，＋∞)（2）(－∞，－2]

【解析】(1)当a＝－1时，f(x)＝2x＋，

因为0<x≤1，所以f(x)＝2x＋≥2＝2，当且仅当x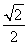＝时，等号成立，

所以函数y＝f(x)的值域是[2，＋∞)．

(2)(解法1)设0<x1<x2≤1，

由f(x1)－f(x2)＝＝2(x1－x2)＋＝，

因为函数y＝f(x)在x∈(0，1]上是减函数，

所以f(x1)－f(x2)>0恒成立，

所以2x1x2＋a<0，即a<－2x1x2在x∈(0，1]上恒成立，

所以a≤－2，即实数a的取值范围是(－∞，－2]．

(解法2)由f(x)＝2x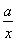－，知f′(x)＝2＋，

因为函数y＝f(x)在x∈(0，1]上是减函数，

所以f′(x)＝2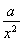＋≤0在x∈(0，1]上恒成立，

即a≤－2x2在x∈(0，1]上恒成立，

所以a≤－2，即实数a的取值范围是(－∞，－2]．