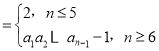Question

【题目】《复仇者联盟4：终局之战》是安东尼·罗素和乔·罗素执导的美国科幻电影，改编自美国漫威漫画，自2019年4月24日上映以来票房火爆.某电影院为了解在该影院观看《复仇者联盟4》的观众的年龄构成情况，随机抽取了100名观众的年龄，并分成，，，，，，七组，得到如图所示的频率分布直方图.

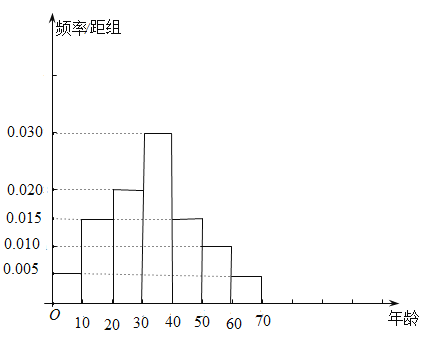
（1）求这100名观众年龄的平均数（同一组数据用该区间的中点值作代表）、中位数；

（2）该电影院拟采用抽奖活动来增加趣味性，观众可以选择是否参与抽奖活动（不参与抽奖活动按原价购票），活动方案如下：每张电影票价格提高10元，同时购买这样电影票的每位观众可获得3次抽奖机会，中奖1次则奖励现金元，中奖2次则奖励现金元，中奖三次则奖励现金元，其中且，已知观众每次中奖的概率均为.

①以某观众三次抽奖所获得的奖金总额的数学期望为评判依据，若要使抽奖方案对电影院有利，则最高可定为多少；

②据某时段内的统计，当时该电影院有600名观众选择参加抽奖活动，并且每增加1元，则参加抽奖活动的观众增加100人.设该时间段内观影的总人数不变，抽奖活动给电影院带来的利润的期望为，求的最大值.

Answer 1

【答案】（1）；（2）①最高定为17元，才能使抽奖方案对电影院有利，②时利润最大，为.

【解析】

（1）由频率分布直方图求平均数以及中位数的方法求解即可；

（2）①设观众三次抽奖所获得的奖金总额为随机变量，可能的取值为0，，，，求出可能取值对应的概率，得出期望，使期望小于等于10，得出对电影院有利时的最大值；

②由期望的值以及题设条件得出的表达式，根据二次函数的性质，得出的最大值.

（1）平均数，

前三组的频率之和为

前四组为

故中位数落在第4组

设中位数为，则

解得，即中位数为.

（2）①设观众三次抽奖所获得的奖金总额为随机变量，可能的取值为0，，，

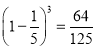
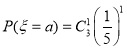
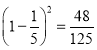
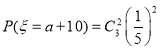
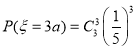
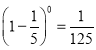
所以，

令，解得

所以最高定为17元，才能使抽奖方案对电影院有利.

②.

为二次函数，其对称轴

时，，时，.

，因此时利润最大，为