题目内容
已知A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD="2AB=6," 则该球的表面积为( )
A.16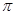 B.24
B.24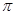 C.48
C.48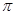 D.32
D.32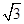
【答案】
C
【解析】
试题分析:根据题意,画出几何体的图形(如图),

把A、B、C、D扩展为三棱柱,上下底面中心连线的中点与A的距离为球的半径。
AD=2AB=6,OE=3,△ABC是正三角形,
所以AE= ,
,
AO=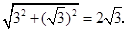
所求球的表面积为48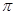 ,故选C。
,故选C。
考点:球、三棱柱的几何特征,球的表面积公式
点评:中档题,本题综合考查球及其内接几何体体的关系,利用割补法结合球内接多面体的几何特征,求出球的半径是解题的关键。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目