题目内容
已知函数 。
。
(Ⅰ)确定 在
在 上的单调性;
上的单调性;
(Ⅱ)设 在
在 上有极值,求
上有极值,求 的取值范围。
的取值范围。
(Ⅰ)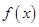 在
在 上单调递减(Ⅱ)
上单调递减(Ⅱ) 的取值范围是
的取值范围是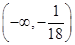
解析试题分析:(Ⅰ)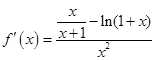
设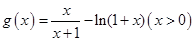 ,则
,则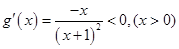
所以,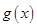 在
在 上单调递减,
上单调递减,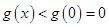 所以,
所以,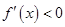 ,
,
因此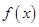 在
在 上单调递减。
上单调递减。
(Ⅱ)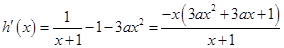
若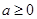 ,任给
,任给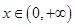 ,
,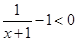 ,
,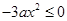
所以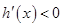 ,
,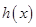 在
在 上单调递减,无极值;
上单调递减,无极值;
若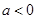 ,
,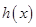 在
在 上有极值时的充要条件是
上有极值时的充要条件是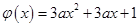 在
在 上有零点,所以
上有零点,所以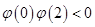 ,解得
,解得
综上, 的取值范围是
的取值范围是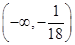
考点:导数的性质,极值。
点评:本题综合考查导数的定义,计算及其在求解函数极值和单调性中的应用。

练习册系列答案
相关题目
 。
。 ,讨论
,讨论 的单调性;
的单调性; 恒有
恒有 ,求
,求 的取值范围。
的取值范围。 (
(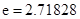 …是自然对数的底数)的最小值为
…是自然对数的底数)的最小值为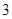 .
. 的值;
的值;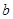
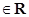 且
且 ,试解关于
,试解关于 的不等式
的不等式 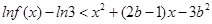 ;
;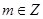 且
且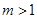 .若存在实数
.若存在实数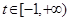 ,使得对任意的
,使得对任意的 ,都有
,都有 ,试求
,试求 的最大值.
的最大值.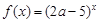 是R上的减函数,命题Q:在
是R上的减函数,命题Q:在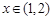 时,不等式
时,不等式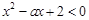 恒成立,若命题“
恒成立,若命题“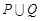 ”是真命题,求实数
”是真命题,求实数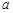 的取值范围.
的取值范围. ,其中
,其中 ,且a≠0.
,且a≠0. 在区间[1,e]上的最小值;
在区间[1,e]上的最小值; 在
在 处取得极小值2.
处取得极小值2. 的解析式;
的解析式; ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围. ,
, ,(
,( 为自然对数的底数).
为自然对数的底数). 时,求函数
时,求函数 的单调区间;
的单调区间; 上恒为正数,求
上恒为正数,求 的最小值;
的最小值; ,在
,在 上总存在两个不同的
上总存在两个不同的 ,使得
,使得 成立,求
成立,求 ,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的
,计划每年砍伐一些树,且每年砍伐面积的百分比相等,当砍伐到面积的一半时,所用时间是10年,为保护生态环境,森林面积至少要保留原面积的 ,已知到今年为止,森林剩余面积为原来的
,已知到今年为止,森林剩余面积为原来的 .
. ,
,
 时,求函数
时,求函数 的极值;
的极值; 的取值范围.
的取值范围.