题目内容
(2010•济南一模)已知函数f(x)=x3-bx2+2cx的导函数的图象关于直线x=2对称.
(1)求b的值;
(2)若函数f(x)无极值求c的取值范围;
(3)若f(x)在x=t处取得极小值,记此极小值为g(t),求g(t)的定义域和值域.
(1)求b的值;
(2)若函数f(x)无极值求c的取值范围;
(3)若f(x)在x=t处取得极小值,记此极小值为g(t),求g(t)的定义域和值域.
分析:(1)先求导函数,根据导函数的图象关于直线x=2对称,可知-
=2,从而可求b的值;
(2)函数f(x)无极值,即导函数为0的方程至多有一解,从而可求c的取值范围;
(3)由(2)知,c<6,f'(x)=0有两个异实根x1,x2,不妨设x1<x2,则x1<2<x2,易得f(x)在x=x1处取极大值,在x=x2处取极小值,且x2>2,可知函数g(t)的定义域为(2,+∞),根据f'(t)=3t2-12t+2c=0得2c=-3t2+12t.从而可得g(t)=f(t)=t3-6t2+(-3t2+12t)t=-2t3+6t2,再利用函数g(t)在区间(2,+∞)内是减函数,可求函数g(t)的值域.
| -2b |
| 6 |
(2)函数f(x)无极值,即导函数为0的方程至多有一解,从而可求c的取值范围;
(3)由(2)知,c<6,f'(x)=0有两个异实根x1,x2,不妨设x1<x2,则x1<2<x2,易得f(x)在x=x1处取极大值,在x=x2处取极小值,且x2>2,可知函数g(t)的定义域为(2,+∞),根据f'(t)=3t2-12t+2c=0得2c=-3t2+12t.从而可得g(t)=f(t)=t3-6t2+(-3t2+12t)t=-2t3+6t2,再利用函数g(t)在区间(2,+∞)内是减函数,可求函数g(t)的值域.
解答:解:(1)f'(x)=3x2-2bx+2c…(1分)
∵函数f'(x)的图象关于直线x=2对称,
∴-
=2,即b=6.…(4分)
(2)由(1)知,f(x)=x3-6x2+2cx,f'(x)=3x2-12x+2c=3(x-2)2+2c-12…(6分)
当c≥6时,f'(x)≥0,此时f(x)无极值 …(8分)
(3)当c<6时,f'(x)=0有两个异实根x1,x2,不妨设x1<x2,则x1<2<x2;
当x<x1时,f'(x)>0,f(x)在区间(-∞,x1)内为增函数;
当x1<x<x2时,f'(x)<0,f(x)在区间(x1,x2)内为减函数;
当x>x2时,f'(x)>0,f(x)在区间(x2,+∞)内为增函数.
所以f(x)在x=x1处取极大值,在x=x2处取极小值 …(10分)
因此,当且仅当c<6时,函数f(x)在x=x2处存在唯一极小值,所以t=x2>2
于是g(t)的定义域为(2,+∞),由f'(t)=3t2-12t+2c=0得2c=-3t2+12t.
于是g(t)=f(t)=t3-6t2+(-3t2+12t)t=-2t3+6t2,t∈(2,+∞)…(12分)
当t>2时,g'(t)=-6t2+12t=-6t(t-2)<0,所以函数g(t)在区间(2,+∞)内是减函数,
故g(t)的值域为(-∞,8).…(14分)
∵函数f'(x)的图象关于直线x=2对称,
∴-
| -2b |
| 6 |
(2)由(1)知,f(x)=x3-6x2+2cx,f'(x)=3x2-12x+2c=3(x-2)2+2c-12…(6分)
当c≥6时,f'(x)≥0,此时f(x)无极值 …(8分)
(3)当c<6时,f'(x)=0有两个异实根x1,x2,不妨设x1<x2,则x1<2<x2;
当x<x1时,f'(x)>0,f(x)在区间(-∞,x1)内为增函数;
当x1<x<x2时,f'(x)<0,f(x)在区间(x1,x2)内为减函数;
当x>x2时,f'(x)>0,f(x)在区间(x2,+∞)内为增函数.
所以f(x)在x=x1处取极大值,在x=x2处取极小值 …(10分)
因此,当且仅当c<6时,函数f(x)在x=x2处存在唯一极小值,所以t=x2>2
于是g(t)的定义域为(2,+∞),由f'(t)=3t2-12t+2c=0得2c=-3t2+12t.
于是g(t)=f(t)=t3-6t2+(-3t2+12t)t=-2t3+6t2,t∈(2,+∞)…(12分)
当t>2时,g'(t)=-6t2+12t=-6t(t-2)<0,所以函数g(t)在区间(2,+∞)内是减函数,
故g(t)的值域为(-∞,8).…(14分)
点评:本题以导函数为载体,考查导函数的性质,考查利用导数求函数的极值,同时考查了函数的定义域与值域,综合性强.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
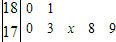 (2010•济南一模)一次选拔运动员,测得7名选手的身高(单位cm)分布茎叶图如图,记录的平均身高为177cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为( )
(2010•济南一模)一次选拔运动员,测得7名选手的身高(单位cm)分布茎叶图如图,记录的平均身高为177cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为( )