题目内容
(2010•济南一模)已知椭圆C:
+
=1(a>b>0)的长轴长为4.
(1)若以原点为圆心、椭圆短半轴为半径的圆与直线y=x+2相切,求椭圆焦点坐标;
(2)若点P是椭圆C上的任意一点,过原点的直线L与椭圆相交于M,N两点,记直线PM,PN的斜率分别为kPM,kPN,当kPM•kPN=-
时,求椭圆的方程.
| x2 |
| a2 |
| y2 |
| b2 |
(1)若以原点为圆心、椭圆短半轴为半径的圆与直线y=x+2相切,求椭圆焦点坐标;
(2)若点P是椭圆C上的任意一点,过原点的直线L与椭圆相交于M,N两点,记直线PM,PN的斜率分别为kPM,kPN,当kPM•kPN=-
| 1 |
| 4 |
分析:(1)由b=
得b=
,再结合椭圆的长轴的长为4,进而根据椭圆中a,b,c的关系得到焦点的坐标.
(2)由题意可设M(x0,y0),N(-x0,-y0),P(x,y),所以有
+
=1,
+
=1,两式相减得:
=-
,再结合两条直线的斜率与题中条件可得答案.
| 2 | ||
|
| 2 |
(2)由题意可设M(x0,y0),N(-x0,-y0),P(x,y),所以有
| ||
| a2 |
| ||
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
y2-
| ||
x2-
|
| b2 |
| a2 |
解答:解:(1)由b=
得b=
…(2分)
又因为2a=4,
所以a=2,又a2=4,b2=2…(4分)
所以c2=a2-b2=2,
∴两个焦点坐标为(
,0),(-
,0)…(6分)
(2)由于过原点的直线L与椭圆相交的两点M,N交于坐标原点对称
不妨设:M(x0,y0),N(-x0,-y0),P(x,y)
因为M,N,P在椭圆上,
所以它们满足椭圆方程,即有
+
=1,
+
=1
两式相减得:
=-
.…(8分)
由题意它们的斜率存在,则kPM=
,kPN=
…(10分)
故所求椭圆的方程为
+y2=1…(12分)
| 2 | ||
|
| 2 |
又因为2a=4,
所以a=2,又a2=4,b2=2…(4分)
所以c2=a2-b2=2,
∴两个焦点坐标为(
| 2 |
| 2 |
(2)由于过原点的直线L与椭圆相交的两点M,N交于坐标原点对称
不妨设:M(x0,y0),N(-x0,-y0),P(x,y)
因为M,N,P在椭圆上,
所以它们满足椭圆方程,即有
| ||
| a2 |
| ||
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
两式相减得:
y2-
| ||
x2-
|
| b2 |
| a2 |
由题意它们的斜率存在,则kPM=
| y-y0 |
| x-x0 |
| y+y0 |
| x+x0 |
|
故所求椭圆的方程为
| x2 |
| 4 |
点评:本题主要考查了椭圆的标准方程,涉及了椭圆与直线的位置关系,以及直线的斜率等问题,综合性强.

练习册系列答案
相关题目
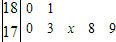 (2010•济南一模)一次选拔运动员,测得7名选手的身高(单位cm)分布茎叶图如图,记录的平均身高为177cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为( )
(2010•济南一模)一次选拔运动员,测得7名选手的身高(单位cm)分布茎叶图如图,记录的平均身高为177cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为( )