题目内容
(2010•济南一模)已知函数f(x)=sin(ωx+?),其中ω>0,|φ|<
|,若a=(1,1),b=(cos?,-sinφ),且
⊥
,又知函数
f(x)的周期为π.
(1)求f(x)的解析式;
(2)若将f(x)的图象向右平移
个单位得到g(x)的图象,求g(x)的单调递增区间.
| π |
| 2 |
| a |
| b |
f(x)的周期为π.
(1)求f(x)的解析式;
(2)若将f(x)的图象向右平移
| π |
| 6 |
分析:(1)根据所给的两个向量垂直,得出它们的数量积为0,求出φ值,再根据周期公式求出ω,最后写出函数的解析式.
(2)根据函数的图象的平移的原则,写出新的函数的解析式,根据正弦曲线的单调区间写出函数的单调递增区间.
(2)根据函数的图象的平移的原则,写出新的函数的解析式,根据正弦曲线的单调区间写出函数的单调递增区间.
解答:解:(1)∵
⊥
,
∴
•
=0…(1分)
∴
•
=cosφ-sinφ=
(
cosφ-
sinφ)=
cos(φ+
)=0…(3分)
∴φ+
=kπ+
,k∈Z,
即φ=kπ+
,k∈Z.
又∵|φ|<
,
∴φ=
.…(5分)
∵函数f(x)的周期T=π,即
=π,ω=2.
∴解析式为f(x)=sin(2x+
)…(6分)
(2)由题意知,函数f(x)的图象向右平移
个单位得到g(x)的图象
∴g(x)=sin[2(x-
)+
]=sin(2x-
)…(8分)
∴g(x)的单调递增区间为2kπ-
≤2x-
≤2kπ+
,k∈Z
解得kπ-
≤x≤kπ+
,k∈Z,…(10分)
∴g(x)的单调递增区间为[kπ-
,kπ+
](k∈Z)…(12分)
| a |
| b |
∴
| a |
| b |
∴
| a |
| b |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
∴φ+
| π |
| 4 |
| π |
| 2 |
即φ=kπ+
| π |
| 4 |
又∵|φ|<
| π |
| 2 |
∴φ=
| π |
| 4 |
∵函数f(x)的周期T=π,即
| 2π |
| ω |
∴解析式为f(x)=sin(2x+
| π |
| 4 |
(2)由题意知,函数f(x)的图象向右平移
| π |
| 6 |
∴g(x)=sin[2(x-
| π |
| 6 |
| π |
| 4 |
| π |
| 12 |
∴g(x)的单调递增区间为2kπ-
| π |
| 2 |
| π |
| 12 |
| π |
| 2 |
解得kπ-
| 5π |
| 24 |
| 7π |
| 24 |
∴g(x)的单调递增区间为[kπ-
| 5π |
| 24 |
| 7π |
| 24 |
点评:本题主要考查了数量积判断两个平面向量的垂直关系、正弦函数的单调性和函数的图象的平移,本题解题的关键是正确写出函数的解析式,这是后面解题的依据,本题是一个中档题目.

练习册系列答案
相关题目
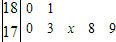 (2010•济南一模)一次选拔运动员,测得7名选手的身高(单位cm)分布茎叶图如图,记录的平均身高为177cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为( )
(2010•济南一模)一次选拔运动员,测得7名选手的身高(单位cm)分布茎叶图如图,记录的平均身高为177cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为( )