题目内容
11.化简:$\frac{si{n}^{2}x+co{s}^{2}x}{(cosx-sinx)^{2}}$.分析 原式利用完全平方公式及同角三角函数基本关系化简即可得到结果.
解答 解:原式=$\frac{si{n}^{2}x+co{s}^{2}x}{co{s}^{2}x+si{n}^{2}x-2sinxcosx}$=$\frac{1}{1-sin2x}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
16.已知x,y是正数,且xy=4,则$\frac{y}{\sqrt{x}}$+$\frac{x}{\sqrt{y}}$取得最小值时,x的值是( )
| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
20.设等差数列{an}的前n项和为Sn.若以a2,a4是方程x2-4x+3=0的两个根,则S5等于( )
| A. | -20 | B. | -10 | C. | 10 | D. | 20 |
1.已知f(x)=3-2x+x2,x∈{-1,1,0,2,3},则f(x)的值域为( )
| A. | {2,3,6} | B. | {1,2,3,6} | C. | {2,3,-3,6} | D. | {2,-2,3} |
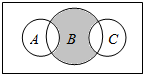 全集为1,A、B、C均为1的子集,则阴影部分表示的集合是(∁I(A∪C))∩B.
全集为1,A、B、C均为1的子集,则阴影部分表示的集合是(∁I(A∪C))∩B.