题目内容
设各项均为正数的数列{an}满足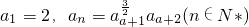 .
.
(Ⅰ)若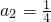 ,求a3,a4,并猜想a2cos的值(不需证明);
,求a3,a4,并猜想a2cos的值(不需证明);
(Ⅱ)记bn=a3a2…an(n∈N*),若bn≥2 对n≥2恒成立,求a2的值及数列{bn}的通项公式.
对n≥2恒成立,求a2的值及数列{bn}的通项公式.
解:(Ⅰ)因a1=2,a2=2-2,故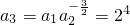 ,
,
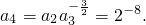
由此有a1=2(-2)0,a2=2(-2)2,a3=2(-2)2,a4=2(-2)3,、
故猜想|an|的通项为an=2(-2)n-1(n∈N*).
(Ⅱ)令xn=log2an,Sn表示xn的前n项和,则bn=2Sn.
由题设知x1=1且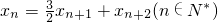 ;①
;①
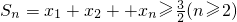 .②
.②
因②式对n=2成立,有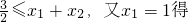
 .③
.③
下用反证法证明: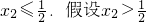 .
.
由①得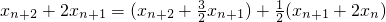 .
.
因此数列|xn+1+2xn|是首项为x2+2,公比为 的等比数列.
的等比数列.
故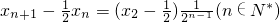 .④
.④
又由①知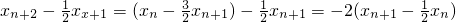 ,
,
因此是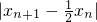 是首项为
是首项为 ,公比为-2的等比数列,
,公比为-2的等比数列,
所以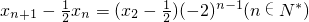 .⑤
.⑤
由④-⑤得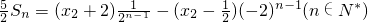 .⑥
.⑥
对n求和得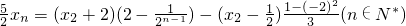 .⑦
.⑦
由题设知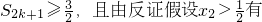
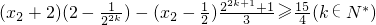 .
.
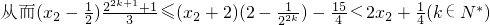 .
.
即不等式22k+1<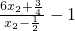
对k∈N*恒成立.但这是不可能的,矛盾.
因此x2≤ ,结合③式知x2=
,结合③式知x2= ,因此a2=2*2=
,因此a2=2*2= .
.
将x2= 代入⑦式得
代入⑦式得
Sn=2- (n∈N*),
(n∈N*),
所以bn=2Sn=22- (n∈N*)
(n∈N*)
分析:(Ⅰ)由题意可知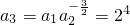 ,
,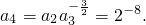 由此可猜想|an|的通项为an=2(-2)n-1(n∈N*).
由此可猜想|an|的通项为an=2(-2)n-1(n∈N*).
(Ⅱ)令xn=log2an,Sn表示xn的前n项和,则bn=2Sn.由题设知x1=1且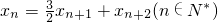 ;
;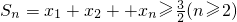 .由此入手能够求出a2的值及数列{bn}的通项公式.
.由此入手能够求出a2的值及数列{bn}的通项公式.
点评:本题考查数列性质的综合运用,解题时要认真审题.仔细解答,避免出错.
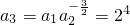 ,
,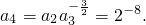
由此有a1=2(-2)0,a2=2(-2)2,a3=2(-2)2,a4=2(-2)3,、
故猜想|an|的通项为an=2(-2)n-1(n∈N*).
(Ⅱ)令xn=log2an,Sn表示xn的前n项和,则bn=2Sn.
由题设知x1=1且
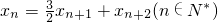 ;①
;①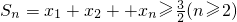 .②
.②因②式对n=2成立,有
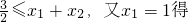
 .③
.③下用反证法证明:
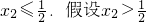 .
.由①得
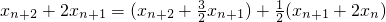 .
.因此数列|xn+1+2xn|是首项为x2+2,公比为
 的等比数列.
的等比数列.故
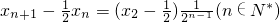 .④
.④又由①知
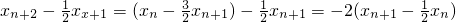 ,
,因此是
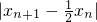 是首项为
是首项为 ,公比为-2的等比数列,
,公比为-2的等比数列,所以
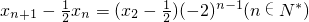 .⑤
.⑤由④-⑤得
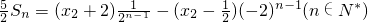 .⑥
.⑥对n求和得
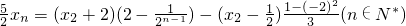 .⑦
.⑦由题设知
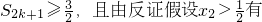
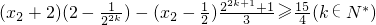 .
.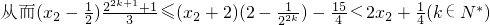 .
.即不等式22k+1<
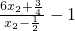
对k∈N*恒成立.但这是不可能的,矛盾.
因此x2≤
 ,结合③式知x2=
,结合③式知x2= ,因此a2=2*2=
,因此a2=2*2= .
.将x2=
 代入⑦式得
代入⑦式得Sn=2-
 (n∈N*),
(n∈N*),所以bn=2Sn=22-
 (n∈N*)
(n∈N*)分析:(Ⅰ)由题意可知
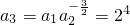 ,
,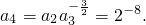 由此可猜想|an|的通项为an=2(-2)n-1(n∈N*).
由此可猜想|an|的通项为an=2(-2)n-1(n∈N*).(Ⅱ)令xn=log2an,Sn表示xn的前n项和,则bn=2Sn.由题设知x1=1且
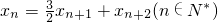 ;
;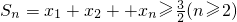 .由此入手能够求出a2的值及数列{bn}的通项公式.
.由此入手能够求出a2的值及数列{bn}的通项公式.点评:本题考查数列性质的综合运用,解题时要认真审题.仔细解答,避免出错.

练习册系列答案
相关题目