题目内容
【题目】已知直三棱柱ABC﹣A1B1C1的底面为正三角形,E,F分别是A1C1 , B1C1上的点,且满足A1E=EC1 , B1F=3FC1 . 
(1)求证:平面AEF⊥平面BB1C1C;
(2)设直三棱柱ABC﹣A1B1C1的棱长均相等,求二面角C1﹣AE﹣B的余弦值.
【答案】
(1)证明:取B1C1的中点G,连结A1G,
∵B1F=3FC1,FG=FC1,∴EF∥A1G,
在等边△A1B1C1中,由G是B1C1的中点,知A1G⊥B1C1,
∴EF⊥B1C1,
∵三棱柱ABC﹣A1B1C1是直棱柱,∴BB1⊥平面A1B1C1,
又∵EF平面A1B1C1,∴BB1⊥EF,
∵BB1∩B1C1=B1,∴EF⊥平面BB1C1C,
又EF平面AEF,∴平面AEF⊥平面BB1C1C
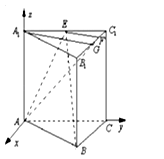
(2)解:(2)以A为坐标原点,以AA1,AC分别为y轴,z轴,建立空间直角坐标系,
设直三棱柱ABC﹣A1B1C1的棱均为2,则A(0,0,0),B( ![]() ),E(0,1,2),
),E(0,1,2),
∴ ![]() =(0,1,2),
=(0,1,2), ![]() =(
=( ![]() ),
),
设 ![]() =(x,y,z)是平面ABE的一个法向量,
=(x,y,z)是平面ABE的一个法向量,
由 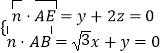 ,取x=﹣2,得
,取x=﹣2,得 ![]() =(﹣2,2
=(﹣2,2 ![]() ,﹣
,﹣ ![]() ),
),
平面AEC1的一个法向量 ![]() =(1,0,0),
=(1,0,0),
设二面角C1﹣AE﹣B的平面角为θ,
则cosθ= ![]() =
= ![]() .
.
∴二面角C1﹣AE﹣B的余弦值为 ![]() .
.

【解析】(1)取B1C1的中点G,连结A1G,推导出EF∥A1G,A1G⊥B1C1 , 从而EF⊥B1C1 , 由三棱柱ABC﹣A1B1C1是直棱柱,得到BB1⊥EF,从而EF⊥平面BB1C1C,由此能证明平面AEF⊥平面BB1C1C.(2)以A为坐标原点,以AA1 , AC分别为y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角C1﹣AE﹣B的余弦值.

