题目内容
7.已知x≥1,y≥0,集合A={(x,y)|x+y≤4},B={(x,y)|y=kx-1},如果A∩B≠∅,则k的取值范围是$[\frac{1}{4},4]$.分析 由题意作出可行域,把A∩B≠Φ转化为直线y=kx-1与可行域有公共点,然后利用两点求直线的斜率得答案.
解答 解:由$\left\{\begin{array}{l}{x≥1}\\{y≥0}\\{x+y≤4}\end{array}\right.$作出可行域如图,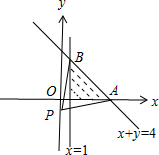
要使A∩B≠∅,则直线y=kx-1与可行域有公共点,
联立$\left\{\begin{array}{l}{x=1}\\{x+y=4}\end{array}\right.$,得B(1,3),
又A(4,0),
直线y=kx-1过定点P(0,-1),
${k}_{PA}=\frac{-1-0}{0-4}=\frac{1}{4}$,${k}_{PB}=\frac{-1-3}{0-1}=4$.
∴k的取值范围是$[\frac{1}{4},4]$.
故答案为:$[\frac{1}{4},4]$.
点评 本题考查了集合运算,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
17.设P为双曲线C:x2-y2=1上一点,F1、F2分别为双曲线C的左右焦点,若cos∠F1PF2=$\frac{1}{3}$,则△PF1F2的外接圆的半径为( )
| A. | $\frac{3}{2}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | 9 |
18.已知实数x∈{1,2,3,4,5,6,7,8},执行如图所示的程序框图,则输出的x不小于121的概率为( )
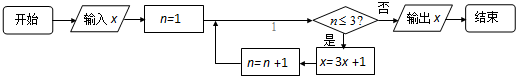
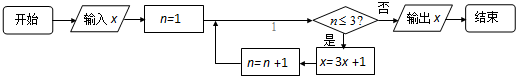
| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{7}{8}$ | D. | $\frac{1}{2}$ |
2.执行如图的程序框图,当输入25时,则该程序运行后输出的结果是( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
12.执行如图的程序框图,若输入a=1,b=1,c=-1,则输出的结果满足( )


| A. | 0<e<1,f>1 | B. | -1<e<0,1<f<2 | C. | -2<e<-1,0<f<1 | D. | 无解 |