题目内容
已知a>0,设p:函数y=ax在R上单调递减;命题q:方程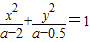 表示的曲线是双曲线,如果“p或q”为真,“p且q”为假,求a的取值范围.
表示的曲线是双曲线,如果“p或q”为真,“p且q”为假,求a的取值范围.
【答案】分析:先求p为真,q为真时,a的范围,再将“p或q”为真,“p且q”为假,转化为p真q假,或p假q真,构建不等式组,即可求得a的取值范围.
解答:解:若p为真,则0<a<1,
若q为真,则(a-2)(a-0.5)<0,解得0.5<a<2
∵“p或q”为真,“p且q”为假,
∴p真q假,或p假q真
若p真q假,则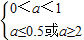 ,∴0<a≤0.5
,∴0<a≤0.5
若p假q真,则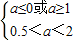 ,∴1≤a<2.
,∴1≤a<2.
综上所述,a∈(0,0.5]∪[1,2)
点评:本题以命题为载体,考查复合命题的真假,考查解不等式,解题的关键是将“p或q”为真,“p且q”为假,转化为p真q假,或p假q真.
解答:解:若p为真,则0<a<1,
若q为真,则(a-2)(a-0.5)<0,解得0.5<a<2
∵“p或q”为真,“p且q”为假,
∴p真q假,或p假q真
若p真q假,则
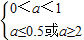 ,∴0<a≤0.5
,∴0<a≤0.5若p假q真,则
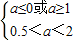 ,∴1≤a<2.
,∴1≤a<2.综上所述,a∈(0,0.5]∪[1,2)
点评:本题以命题为载体,考查复合命题的真假,考查解不等式,解题的关键是将“p或q”为真,“p且q”为假,转化为p真q假,或p假q真.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
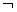 Q”为真命题,求实数a的取值范围。
Q”为真命题,求实数a的取值范围。