题目内容
已知sin(α-β)=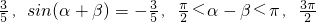 <α+β<2π,则cos2β=________.
<α+β<2π,则cos2β=________.
-1
分析:根据同角三角函数的基本关系求出cos(α-β)、cos(α+β)的值,由cos2β=cos[(α+β)-(α-β)]利用两角差的余弦公式,运算求得结果.
解答:∵sin(α-β)= ,
, <α-β<π,
<α-β<π,
∴cos(α-β)=- .
.
∵ <α+β<2π,sin(α+β)=-
<α+β<2π,sin(α+β)=- ,
,
∴cos(α+β)= .
.
故 cos2β=cos[(α+β)-(α-β)]=cos(α+β)cos(α-β)+sin(α+β)sin(α-β)
= ×(-
×(- )+(-
)+(- )
) =-1,
=-1,
故答案为-1.
点评:本题主要考查同角三角函数的基本关系,两角差的余弦公式的应用,注意三角函数值的符号,这是解题的易错点,
属于中档题.
分析:根据同角三角函数的基本关系求出cos(α-β)、cos(α+β)的值,由cos2β=cos[(α+β)-(α-β)]利用两角差的余弦公式,运算求得结果.
解答:∵sin(α-β)=
 ,
, <α-β<π,
<α-β<π,∴cos(α-β)=-
 .
.∵
 <α+β<2π,sin(α+β)=-
<α+β<2π,sin(α+β)=- ,
,∴cos(α+β)=
 .
.故 cos2β=cos[(α+β)-(α-β)]=cos(α+β)cos(α-β)+sin(α+β)sin(α-β)
=
 ×(-
×(- )+(-
)+(- )
) =-1,
=-1,故答案为-1.
点评:本题主要考查同角三角函数的基本关系,两角差的余弦公式的应用,注意三角函数值的符号,这是解题的易错点,
属于中档题.

练习册系列答案
相关题目