题目内容
)如图,AC 是圆 O 的直径,点 B 在圆 O 上,∠BAC=30°,BM⊥AC交 AC 于点 M,EA⊥平面ABC,FC//EA,AC=4,EA=3,FC=1.
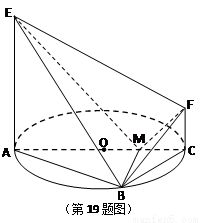
(I)证明:EM⊥BF;
(II)求平面 BEF 与平面ABC 所成锐二面角的余弦值.
【答案】
(1)略(2)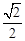 .
.
【解析】本试题主要是考查了线线的垂直的证明和二面角的平面角的求解的综合运用。
(1)根据已知条件可以建立空间直角坐标系,然后借助于向量的数量积为零来证明线线的垂直问题。
(2)而第二问的二面角需要求解平面的法向量,运用法向量和法向量的夹角来表示二面角的平面角的大小,体现了向量的代数法手段的好处,。避免了复杂的空间位置关系的运用。
解:(1)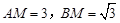 .如图,以
.如图,以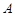 为坐标原点,垂直于
为坐标原点,垂直于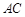 、
、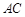 、
、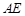 所在的直线为
所在的直线为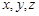 轴建立空间直角坐标系.
轴建立空间直角坐标系.

由已知条件得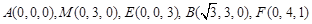 ,
,
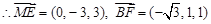 .由
.由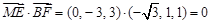 ,
,
得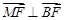 ,
,
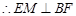 . ……………6分
. ……………6分
(2)由(1)知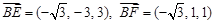 .
.
设平面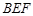 的法向量为
的法向量为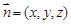 ,由
,由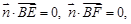 得
得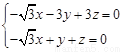 ,
,
令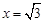 得
得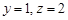 ,
,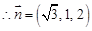 ,
,
由已知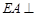 平面
平面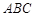 ,所以取面
,所以取面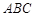 的法向量为
的法向量为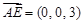 ,
,
设平面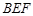 与平面
与平面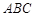 所成的锐二面角为
所成的锐二面角为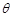 ,则
,则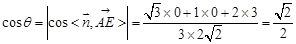 ,平面
,平面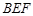 与平面
与平面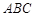 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为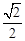 .
.

练习册系列答案
相关题目
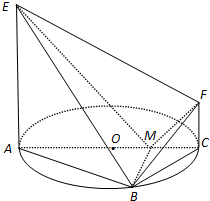 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.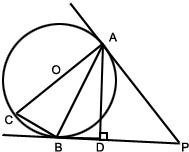 如图,AC是圆O的直径,AC=10厘米,PA,PB是圆O的切线,A,B为切点,过A作AD⊥BP,交BP于D点,连接AB,BC.
如图,AC是圆O的直径,AC=10厘米,PA,PB是圆O的切线,A,B为切点,过A作AD⊥BP,交BP于D点,连接AB,BC.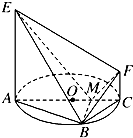 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.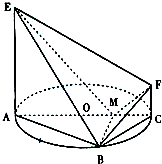 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.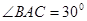 ,
,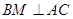 交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,
交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,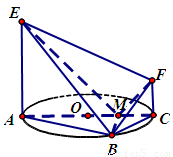
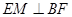 ;
;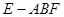 的体积
的体积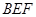 和平面
和平面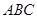 所成的锐二面角的正切值.
所成的锐二面角的正切值.