题目内容
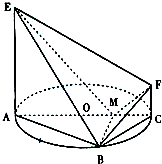 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.(1)证明:EM⊥BF;
(2)求平面BEF与平面ABC所成的锐二面角的余弦值;
(3)当
| EF |
| EP |
分析:(1)根据线面垂直得到线与线垂直,根据直径所对的圆周角是直角,得到两个三角形是等腰直角三角形,利用线面垂直的判定定理得到结果;
(2)延长EF交AC于G,连BG,过C作CH⊥BG,连接FH.,做出∠FHC为平面BEF与平面ABC所成的二面角的平面角,求出平面角;
(3)建立空间直角坐标系,求出平面ABE的法向量,
的坐标,利用距离公式可得结论.
(2)延长EF交AC于G,连BG,过C作CH⊥BG,连接FH.,做出∠FHC为平面BEF与平面ABC所成的二面角的平面角,求出平面角;
(3)建立空间直角坐标系,求出平面ABE的法向量,
| AP |
解答: (1)证明:∵EA⊥平面ABC,BM?平面ABC,∴EA⊥BM.
(1)证明:∵EA⊥平面ABC,BM?平面ABC,∴EA⊥BM.
又∵BM⊥AC,EA∩AC=A,∴BM⊥平面ACFE,
而EM?平面ACFE,∴BM⊥EM.∵AC是圆O的直径,∴∠ABC=90°.
又∵∠BAC=30°,AC=4,∴AB=2
,BC=2,AM=3,CM=1.∵EA⊥平面ABC,FC∥EA,
=
∴FC⊥平面ABC.∴△EAM与△FCM都是等腰直角三角形.
∴∠EMA=∠FMC=45°.∴∠EMF=90°,即EM⊥MF.
∵MF∩BM=M,∴EM⊥平面MBF.
而BF?平面MBF,∴EM⊥BF.
(2)解:延长EF交AC于G,连BG,过C作CH⊥BG,连接FH.
由(1)知FC⊥平面ABC,BG?平面ABC,∴FC⊥BG.
而FC∩CH=C,∴BG⊥平面FCH.∵FH?平面FCH,∴FH⊥BG,
∴∠FHC为平面BEF与平面ABC所成的二面角的平面角.
在Rt△ABC中,∵∠BAC=30°,AC=4,
∴BM=AB•sin30°=
.
由
=
=
,得GC=2.∵BG=
=2
.
又∵△GCH∽△GBM,∴
=
,则CH=
=1.
∴△FCH是等腰直角三角形,∠FHC=45°.
∴平面BEF与平面ABC所成的锐二面角的余弦值为
.
(3)解:以A为坐标原点,垂直于AC的直线,AC,AE所在直线为x,y,z轴建立空间直角坐标系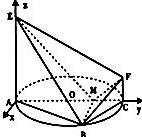
设P(0,y0,z0),∵E(0,0,3),F(0,4,1)
∴
=(0,4,-2)∴
=(0,y0,z0-3)
∵
=6
,∴
,∴
∴P(O,
,
),
∴
=(0,
,
)
∵BC⊥AB,BC⊥AE,AB∩AE=A
∴BC⊥平面ABE
∴平面ABE的一个法向量为
=(-
,1,0)
∴d=
=
.
 (1)证明:∵EA⊥平面ABC,BM?平面ABC,∴EA⊥BM.
(1)证明:∵EA⊥平面ABC,BM?平面ABC,∴EA⊥BM.又∵BM⊥AC,EA∩AC=A,∴BM⊥平面ACFE,
而EM?平面ACFE,∴BM⊥EM.∵AC是圆O的直径,∴∠ABC=90°.
又∵∠BAC=30°,AC=4,∴AB=2
| 3 |
| FC |
| EA |
| 1 |
| 3 |
∴FC⊥平面ABC.∴△EAM与△FCM都是等腰直角三角形.
∴∠EMA=∠FMC=45°.∴∠EMF=90°,即EM⊥MF.
∵MF∩BM=M,∴EM⊥平面MBF.
而BF?平面MBF,∴EM⊥BF.
(2)解:延长EF交AC于G,连BG,过C作CH⊥BG,连接FH.
由(1)知FC⊥平面ABC,BG?平面ABC,∴FC⊥BG.
而FC∩CH=C,∴BG⊥平面FCH.∵FH?平面FCH,∴FH⊥BG,
∴∠FHC为平面BEF与平面ABC所成的二面角的平面角.
在Rt△ABC中,∵∠BAC=30°,AC=4,
∴BM=AB•sin30°=
| 3 |
由
| FC |
| EA |
| GC |
| GA |
| 1 |
| 3 |
| BM2+MG2 |
| 3 |
又∵△GCH∽△GBM,∴
| GC |
| BG |
| CH |
| BM |
| GC•BM |
| BG |
∴△FCH是等腰直角三角形,∠FHC=45°.
∴平面BEF与平面ABC所成的锐二面角的余弦值为
| ||
| 2 |
(3)解:以A为坐标原点,垂直于AC的直线,AC,AE所在直线为x,y,z轴建立空间直角坐标系

设P(0,y0,z0),∵E(0,0,3),F(0,4,1)
∴
| EF |
| EP |
∵
| EF |
| EP |
|
|
∴P(O,
| 2 |
| 3 |
| 8 |
| 3 |
∴
| AP |
| 2 |
| 3 |
| 8 |
| 3 |
∵BC⊥AB,BC⊥AE,AB∩AE=A
∴BC⊥平面ABE
∴平面ABE的一个法向量为
| BC |
| 3 |
∴d=
|
| ||||
|
|
| 1 |
| 3 |
点评:本题主要考查空间点、线、面位置关系,二面角等基础知识,考查应用向量知识解决数学问题的能力,考查空间想象能力、运算能力和推理论证能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.
如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.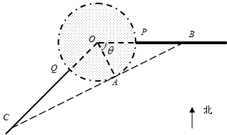 如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.
如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.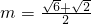 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?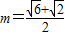 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?
 与直线
与直线 的夹角大小为
的夹角大小为
 B.(不等式选讲)要使关于x的不等式
B.(不等式选讲)要使关于x的不等式 在实数
在实数