题目内容
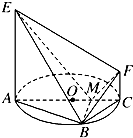 如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.
如图,AC是圆O的直径,点B在圆O上,∠BAC=30°,BM⊥AC交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1.(1)证明:EM⊥BF;
(2)(文科)求三棱锥E-ABF的体积
(理科)求平面BEF与平面ABC所成的锐二面角的正切值.
分析:(1)根据线面垂直得到线与线垂直,根据直径所对的圆周角是直角,得到两个三角形是等腰直角三角形,有线面垂直得到结果.
(2)(文科)由VE-ABF=VB-AEF=
MB•S△AEF,求出底面面积和高,代入棱锥体积公式可得答案.
(理科)做出辅助线,延长EF交AC于G,连BG,过C作CH⊥BG,连接FH.,做出∠FHC为平面BEF与平面ABC所成的二面角的平面角,求出平面角.
(2)(文科)由VE-ABF=VB-AEF=
| 1 |
| 3 |
(理科)做出辅助线,延长EF交AC于G,连BG,过C作CH⊥BG,连接FH.,做出∠FHC为平面BEF与平面ABC所成的二面角的平面角,求出平面角.
解答:证明:(1)∵EA⊥面ABC,BM?面ABC,
∴EA⊥MB
∴MB⊥AC,AC∩EA=A,
∴MB⊥面ACEF
∵EM?面ACEF,
∴EM⊥MB
在直角梯形ACEF中,EA=3,FC=1,AC=4
∴EF=2
在Rt△ABC中,
∵∠BAC=30°,BM⊥AC
∴AM=3,CM=1
∴EM=3
,MF=
∵EF2=EM2+MF2
∴EM⊥MF,又MB∩MF=M
∴EM⊥面MBF,
∵BF?面MBF
∴EM⊥BF…(8分)
解:(2)
(文科) 由(1)知,MB⊥面ACFE
∴VE-ABF=VB-AEF=
MB•S△AEF
在直角梯形ACEF中,
S△AEF=
AE•AC=6,MB=
∴VE-ABF=2
…(14分)
(理科)延长EF交AC于H,连结BH
过C做CG⊥BH,垂足G
FC∥EA,EA⊥面ABC
∴FC⊥面ABC,
∵BH?面ABC
∴BH⊥FC,∵FC∩CG=C
∴BH⊥面FCG,∵FG?面FCG
∴BH⊥FG
∴∠CGF为平面BEF与平面ABC所成的二面角的平面角
在直角梯形ACEF中,CH=2
在△BCH中,CH=2,BC=2,∠BCH=120°
∴CG=1,
在Rt△CGF中,FC=1
∴∠CGF=45°
平面BEF与平面ABC所成的锐二面角正切值为1…(14分)
∴EA⊥MB
∴MB⊥AC,AC∩EA=A,
∴MB⊥面ACEF
∵EM?面ACEF,
∴EM⊥MB
在直角梯形ACEF中,EA=3,FC=1,AC=4
∴EF=2
| 5 |
在Rt△ABC中,
∵∠BAC=30°,BM⊥AC
∴AM=3,CM=1
∴EM=3
| 2 |
| 2 |
∵EF2=EM2+MF2
∴EM⊥MF,又MB∩MF=M
∴EM⊥面MBF,
∵BF?面MBF
∴EM⊥BF…(8分)
解:(2)
(文科) 由(1)知,MB⊥面ACFE
∴VE-ABF=VB-AEF=
| 1 |
| 3 |
在直角梯形ACEF中,
S△AEF=
| 1 |
| 2 |
| 3 |
∴VE-ABF=2
| 3 |
(理科)延长EF交AC于H,连结BH
过C做CG⊥BH,垂足G
FC∥EA,EA⊥面ABC
∴FC⊥面ABC,
∵BH?面ABC
∴BH⊥FC,∵FC∩CG=C
∴BH⊥面FCG,∵FG?面FCG
∴BH⊥FG
∴∠CGF为平面BEF与平面ABC所成的二面角的平面角
在直角梯形ACEF中,CH=2
在△BCH中,CH=2,BC=2,∠BCH=120°
∴CG=1,
在Rt△CGF中,FC=1
∴∠CGF=45°
平面BEF与平面ABC所成的锐二面角正切值为1…(14分)
点评:本题主要考查空间点、线、面位置关系,二面角等基础知识,考查应用向量知识解决数学问题的能力,考查空间想象能力、运算能力和推理论证能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.
如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.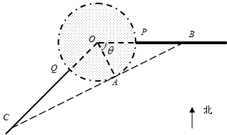 如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.
如图,某城市设立以城中心O为圆心、r公里为半径的圆形保护区,从保护区边缘起,在城中心O正东方向上有一条高速公路PB、西南方向上有一条一级公路QC,现要在保护区边缘PQ弧上选择一点A作为出口,建一条连接两条公路且与圆O相切的直道BC.已知通往一级公路的道路AC每公里造价为a万元,通往高速公路的道路AB每公里造价是m2a万元,其中a,r,m为常数,设∠POA=θ,总造价为y万元.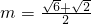 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?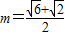 时,如何确定A点的位置才能使得总造价最低?
时,如何确定A点的位置才能使得总造价最低?
 与直线
与直线 的夹角大小为
的夹角大小为
 B.(不等式选讲)要使关于x的不等式
B.(不等式选讲)要使关于x的不等式 在实数
在实数