题目内容
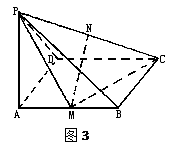
((本题14分)如图3,四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=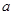 。
。
(Ⅰ)求证:MN//平面PAD;
(Ⅱ)求证:平面PMC⊥平面PCD;
(Ⅲ)若二面角P—MC—A是60°的二面角,求四棱锥P—ABCD的体积。
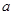 。
。(Ⅰ)求证:MN//平面PAD;
(Ⅱ)求证:平面PMC⊥平面PCD;
(Ⅲ)若二面角P—MC—A是60°的二面角,求四棱锥P—ABCD的体积。

证明:(Ⅰ)如答图所示,⑴设PD的中点为E,连结AE、NE,
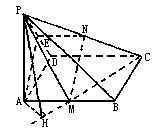
由N为PD的中点知EN
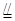
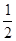 DC,
DC,又ABCD是矩形,∴DC
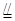 AB,∴EN
AB,∴EN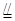
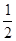 AB
AB又M是AB的中点,∴EN
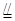 AN, …3分
AN, …3分∴AMNE是平行四边形
∴MN∥AE,而AE
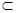 平面PAD,NM
平面PAD,NM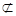 平面PAD
平面PAD∴MN∥平面PAD …4分
(Ⅱ)∵PA=AD,∴AE⊥PD,
又∵PA⊥平面ABCD,CD
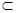 平面ABCD,
平面ABCD,∴CD⊥PA,而CD⊥AD,∴CD⊥平面PAD …6分
∴CD⊥AE, ∵PD∩CD=D,∴AE⊥平面PCD,
∵MN∥AE,∴MN⊥平面PCD,又MN
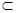 平面PMC,
平面PMC,∴平面PMC⊥平面PCD. …8分
(Ⅲ)解:过A作AH⊥CM,交CM的延长线于H,连PH.
∵PA⊥平面ABCD,AH⊥CH,∴PH⊥CH, ∴∠PHA是二面角P-MC-A的平面角,
∴AH=
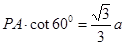 … 10分
… 10分又∵Rt△MHA∽Rt△MBC,
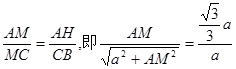
∴
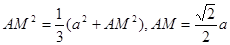
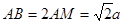 …12分
…12分∴
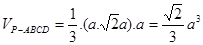 …
… 14分
14分解法二:(Ⅱ)以A为原点,AB,AD,AP所在直线分别为
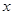 轴、
轴、 轴、
轴、 轴建系
轴建系设AB="b " (b>0) 面PMC法向量
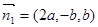 面PDC法向量
面PDC法向量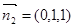
∵
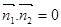 ∴面PMC
∴面PMC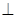 面PDC …8分
面PDC …8分(Ⅲ)面MCA法向量
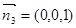 ∵二面角P—MC—A是60°的二面角
∵二面角P—MC—A是60°的二面角∴
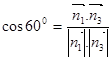 ∴
∴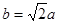 …12分
…12分∴
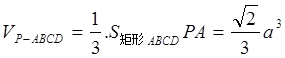 …
… 14分
14分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
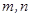 是不同的直线,
是不同的直线,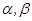 是不重合的平面,给出下面三个命题:
是不重合的平面,给出下面三个命题: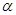 //
//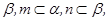 则
则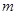 //
//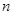 .
.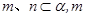 //
//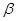 ,
,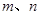 是两条异面直线,若
是两条异面直线,若


 ∥平面
∥平面 ,
, ,那么过点
,那么过点 且平行于
且平行于 内
内
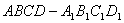 中,以顶点
中,以顶点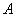 为端点的三条棱长都是
为端点的三条棱长都是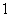 ,且它们彼此的夹角都是
,且它们彼此的夹角都是 ,则以
,则以



 、N分别是AF、BC的中点.请把下面几种正确说法的序号填在横线上 .
、N分别是AF、BC的中点.请把下面几种正确说法的序号填在横线上 .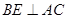 ;
;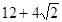 ;
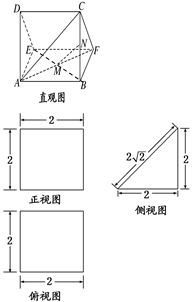
;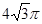 .
.
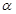 内的两条直线垂直,则
内的两条直线垂直,则 .
. ,
,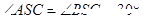 ,则棱锥S-ABC的体积为 ( )
,则棱锥S-ABC的体积为 ( )

