题目内容
【题目】已知动圆![]() 过定点
过定点![]() 且与
且与![]() 轴相切,点
轴相切,点![]() 关于圆心
关于圆心![]() 的对称点为
的对称点为![]() ,动点
,动点![]() 的轨迹记为
的轨迹记为![]() .
.
(1)求![]() 的方程;
的方程;
(2)设直线![]() :
:![]() 与曲线
与曲线![]() 交于点
交于点![]() 、
、![]() ;直线
;直线![]() :
:![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,其中
,其中![]() ,以
,以![]() 、
、![]() 为直径的圆
为直径的圆![]() 、
、![]() (
(![]() 、
、![]() 为圆心)的公共弦所在直线记为
为圆心)的公共弦所在直线记为![]() ,求
,求![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)设![]() ,则
,则![]() ,结合直线与圆相切的充分必要条件可得
,结合直线与圆相切的充分必要条件可得![]() .整理化简,则轨迹方程为
.整理化简,则轨迹方程为![]() .
.
(2)设![]() ,
,![]() ,联立直线与抛物线的方程可得
,联立直线与抛物线的方程可得![]() ,
,
![]() ,结合韦达定理可得以
,结合韦达定理可得以![]() 为直径的圆的方程是:
为直径的圆的方程是:![]() ,化简可得
,化简可得![]() ,同理可得以
,同理可得以![]() 为直径的圆的方程是:
为直径的圆的方程是:![]() ,两式作差可得
,两式作差可得![]() 的方程是:
的方程是:![]() .结合点到直线距离公式可得
.结合点到直线距离公式可得![]() ,则所求距离最小值为
,则所求距离最小值为![]() .
.
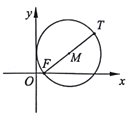
详解:(1)如图,设![]() ,则
,则![]() ,
,
由题可知![]() ,动圆
,动圆![]() 与
与![]() 轴相切,得
轴相切,得![]() .
.
即![]() .
.
化简得:![]() .
.
(2)设![]() ,
,![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,![]() ,
,
则:![]() ,
,
且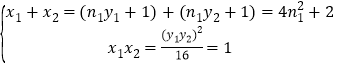 ①
①
设![]() 是
是![]() 上的任意一点.
上的任意一点.
由![]() 得以
得以![]() 为直径的圆的方程是:
为直径的圆的方程是:
![]() ,
,
将①式代入上式,化简得:![]() ②
②
同理以![]() 为直径的圆的方程是:
为直径的圆的方程是:![]() ③
③
②![]() ③得
③得![]() 的方程是:
的方程是:![]() .
.
又![]() ,
,
![]() 到
到![]() 的距离:
的距离:![]()
当![]() 时,所求距离最小值为
时,所求距离最小值为![]() .
.

【题目】红星海水养殖场进行某水产品的新旧养殖方法的产量对比,收货时在旧养殖的大量网箱中随机抽取![]() 个网箱,在新养殖法养殖的大量网箱中也随机抽取
个网箱,在新养殖法养殖的大量网箱中也随机抽取![]() 个网箱,测量各箱水产品的产量,得样本频率分布直方图如下:
个网箱,测量各箱水产品的产量,得样本频率分布直方图如下:

(1)填写下列列联表,并根据列联表判断是否有![]() 的把握认为箱产量与养殖方法有关.
的把握认为箱产量与养殖方法有关.
养殖法 箱产量 | 箱产量 | 箱产量 | 总计 |
旧养殖法 | |||
新养殖法 | |||
总计 |
(2)设两种养殖方法的产量互相独立,记![]() 表示事件:“旧养殖法的箱产量低于
表示事件:“旧养殖法的箱产量低于![]() ,新养殖法的箱产量不低于
,新养殖法的箱产量不低于![]() ”,估计
”,估计![]() 的概率;
的概率;
(3)某水产批发户从红星海水养殖场用新养殖法养殖的大量网箱水产品中购买了![]() 个网箱的水产品,记
个网箱的水产品,记![]() 表示箱产量位于区间
表示箱产量位于区间![]() 的网箱个数,以上样本在相应区间的频率代替概率,求
的网箱个数,以上样本在相应区间的频率代替概率,求![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
(![]() ,其中
,其中![]() )
)
【题目】近期,某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付,某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),绘制了如图所示的散点图:
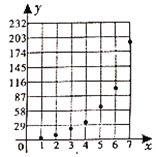
(I)根据散点图判断在推广期内,![]() 与
与![]() (c,d为为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(c,d为为大于零的常数)哪一个适宜作为扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(I)的判断结果求y关于x的回归方程,并预测活动推出第8天使用扫码支付的人次.
参考数据:
|
|
|
|
|
|
|
4 | 62 | 1.54 | 2535 | 50.12 | 140 | 3.47 |
其中![]() ,
,![]()
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: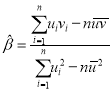 ,
,![]() 。
。