题目内容
设双曲线C:
-y2=1的左、右顶点分别为A1、A2,垂直于x轴的直线l与双曲线C交于不同的两点P、Q.若直线l与x轴正半轴的交点为M,且
•
=1,则点M的坐标为( )
| x2 |
| 2 |
| A1P |
| A2Q |
A、(
| ||
| B、(2,0) | ||
C、(
| ||
| D、(3,0) |
分析:先求出点A1、A2的坐标,设出点P、Q以及M的坐标;利用向量的坐标运算求出关于点M坐标的等式,再结合P(a,b)在双曲线上,联立即可求出点M的坐标.
解答:解:由题得:A1(-
,0),A2(
,0),
设M(a,0),P(a,b),Q(a,-b).则a>0.
所以
=(a+
,b),
=(a-
,-b).
∵
•
=1,
∴(a+
)(a-
)-b2=1,即a2-b2=3 ①
又因为P(a,b)在双曲线上,故有
-b2=1 ②
联立①②得:a2=4,故a=2.
故选B.
| 2 |
| 2 |
设M(a,0),P(a,b),Q(a,-b).则a>0.
所以
| A1P |
| 2 |
| A2Q |
| 2 |
∵
| A1P |
| A2Q |
∴(a+
| 2 |
| 2 |
又因为P(a,b)在双曲线上,故有
| a2 |
| 2 |
联立①②得:a2=4,故a=2.
故选B.
点评:本题主要考查直线与圆锥曲线的综合问题以及向量的坐标运算.解决本题的关键在于对向量的坐标运算的熟练掌握.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
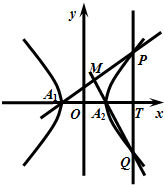 设双曲线C:
设双曲线C: