题目内容
设双曲线C:| x2 |
| 2 |
(1)若直线m与x轴正半轴的交点为T,且
| A1P |
| A2Q |
(2)求直线A1P与A2Q的交点M的轨迹E的方程.
分析:(1)利用已知
•
=1,得到P的坐标满足的等式,又点P在双曲线上得到p的坐标满足的另一个等式,解方程组求出p的坐标,进一步得到T的坐标.
(2)利用A1,P,M三点共线,得:(x0+
)y=y0(x+
),由A2,Q,M三点共线,(x0-
)y=-y0(x-
),
从中得到x0=
,y0=
,又P(x0,y0)在双曲线上,
代入双曲线方程求出轨迹方程.
| A1P |
| A2Q |
(2)利用A1,P,M三点共线,得:(x0+
| 2 |
| 2 |
| 2 |
| 2 |
从中得到x0=
| 2 |
| x |
| ||
| x |
代入双曲线方程求出轨迹方程.
解答:解:(1)由题意得A1(-
,0),A2(
,0),设P(x0,y0),Q(x0,-y0),
则
=(x0+
,y0),
=(x0-
,-y0).
由
•
=1⇒
-
-2=1,
即x02-y02=3,①…(3分)
又P(x0,y0)在双曲线上,则
-
=1.②
联立①、②,解得:x0=±2,由题意,x0>0,
∴x0=2,
∴点T的坐标为(2,0)…(6分)
(2)设直线A1P与A2Q的交点M的坐标为(x,y),
由A1,P,M三点共线,得:(x0+
)y=y0(x+
),①
由A2,Q,M三点共线,得:(x0-
)y=-y0(x-
),②
联立①、②,解得:x0=
,y0=
.…(9分)
∵P(x0,y0)在双曲线上,
∴
-(
)2=1
∴轨迹E的方程为
+y2=1(x≠0,y≠0).…(12分)
| 2 |
| 2 |
则
| A1P |
| 2 |
| A2Q |
| 2 |
由
| A1P |
| A2Q |
| x | 2 0 |
| y | 2 0 |
即x02-y02=3,①…(3分)
又P(x0,y0)在双曲线上,则
| ||
| 2 |
| y | 2 0 |
联立①、②,解得:x0=±2,由题意,x0>0,
∴x0=2,
∴点T的坐标为(2,0)…(6分)
(2)设直线A1P与A2Q的交点M的坐标为(x,y),
由A1,P,M三点共线,得:(x0+
| 2 |
| 2 |
由A2,Q,M三点共线,得:(x0-
| 2 |
| 2 |
联立①、②,解得:x0=
| 2 |
| x |
| ||
| x |
∵P(x0,y0)在双曲线上,
∴
(
| ||
| 2 |
| ||
| x |
∴轨迹E的方程为
| x2 |
| 2 |
点评:本题主要考查了直线与圆锥曲线的综合问题,考查了学生对解析几何学知识的综合运用.

练习册系列答案
相关题目
设双曲线C:
-y2=1的左、右顶点分别为A1、A2,垂直于x轴的直线l与双曲线C交于不同的两点P、Q.若直线l与x轴正半轴的交点为M,且
•
=1,则点M的坐标为( )
| x2 |
| 2 |
| A1P |
| A2Q |
A、(
| ||
| B、(2,0) | ||
C、(
| ||
| D、(3,0) |
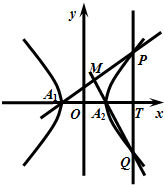 设双曲线C:
设双曲线C: