题目内容
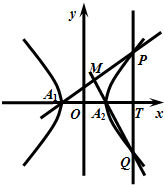 设双曲线C:
设双曲线C:| x2 |
| 2 |
(1)若直线m与x轴正半轴的交点为T,且
| A1P |
| A2Q |
(2)求直线A1P与直线A2Q的交点M的轨迹E的方程;
(3)过点F(1,0)作直线l与(2)中的轨迹E交于不同的两点A、B,设
| FA |
| FB |
| TA |
| TB |
分析:(1)设出P、Q的坐标,求得向量的坐标,利用
•
=1,P(x0,y0)在双曲线上,即可求得结论;
(2)利用三点共线建立方程,利用P(x0,y0)在双曲线上,即可求得轨迹方程;
(3)用坐标表示
+
,利用韦达定理,求得模长,从而可得函数关系式,进而可求其范围.
| A1P |
| A2Q |
(2)利用三点共线建立方程,利用P(x0,y0)在双曲线上,即可求得轨迹方程;
(3)用坐标表示
| TA |
| TB |
解答:解:(1)由题,得A1(-
,0),A2(
,0),
设P(x0,y0),Q(x0,-y0),则
=(x0+
,y0),
=(x0-
,-y0)
由
•
=1,可得
-
=3 …①
又P(x0,y0)在双曲线上,则
-
=1 …②
联立①、②,解得x0=±2
由题意,x0>0,∴x0=2
∴点T的坐标为(2,0)
(2)设直线A1P与直线A2Q的交点M的坐标为(x,y)
由A1、P、M三点共线,得(x0+
)y=y0(x+
) …③
由A2、Q、M三点共线,得(x0-
)y=-y0(x-
) …④
联立③、④,解得x0=
,y0=
∵P(x0,y0)在双曲线上,∴
-(
)2=1
∴轨迹E的方程为
+y2=1(x≠0,y≠0)
(3)由题意直线l的斜率不为0.故可设直线l的方程为x=ky+1代入
+y2=1中,得(k2+2)y2+2ky-1=0
设A(x1,y1),B(x2,y2),则由根与系数的关系,得y1+y2=
…⑤y1y2=
…⑥
∵
=λ
,∴有
=λ(λ<0)
将⑤式平方除以⑥式,得
+
+2=-
,即λ+
+2=-
,
由λ∈[-2,-1],可得λ+
+2≤0
∴-
≤0,∴0≤k2≤
∵
+
=(x1+x2-4,y1+y2)
∴|
+
|2=(x1+x2-4)2+(y1+y2)2=16-
+
令t=
,∵0≤k2≤
,∴
≤
≤
,即t∈[
,
]
∴|
+
|2=f(t)=8t2-28t+16=8(t-
)2-
而t∈[
,
],∴f(t)∈[4,
]
∴|
+
|∈[2,
].
| 2 |
| 2 |
设P(x0,y0),Q(x0,-y0),则
| A1P |
| 2 |
| A2Q |
| 2 |
由
| A1P |
| A2Q |
| x | 2 0 |
| y | 2 0 |
又P(x0,y0)在双曲线上,则
| ||
| 2 |
| y | 2 0 |
联立①、②,解得x0=±2
由题意,x0>0,∴x0=2
∴点T的坐标为(2,0)
(2)设直线A1P与直线A2Q的交点M的坐标为(x,y)
由A1、P、M三点共线,得(x0+
| 2 |
| 2 |
由A2、Q、M三点共线,得(x0-
| 2 |
| 2 |
联立③、④,解得x0=
| 2 |
| x |
| ||
| x |
∵P(x0,y0)在双曲线上,∴
(
| ||
| 2 |
| ||
| x |
∴轨迹E的方程为
| x2 |
| 2 |
(3)由题意直线l的斜率不为0.故可设直线l的方程为x=ky+1代入
| x2 |
| 2 |
设A(x1,y1),B(x2,y2),则由根与系数的关系,得y1+y2=
| -2k |
| k2+2 |
| -1 |
| k2+2 |
∵
| FA |
| FB |
| y1 |
| y2 |
将⑤式平方除以⑥式,得
| y1 |
| y2 |
| y2 |
| y1 |
| 4k2 |
| k2+2 |
| 1 |
| λ |
| 4k2 |
| k2+2 |
由λ∈[-2,-1],可得λ+
| 1 |
| λ |
∴-
| -4k2 |
| k2+2 |
| 2 |
| 7 |
∵
| TA |
| TB |
∴|
| TA |
| TB |
| 28 |
| k2+2 |
| 8 |
| (k2+2)2 |
令t=
| 1 |
| k2+2 |
| 2 |
| 7 |
| 7 |
| 16 |
| 1 |
| k2+2 |
| 1 |
| 2 |
| 7 |
| 16 |
| 1 |
| 2 |
∴|
| TA |
| TB |
| 7 |
| 4 |
| 17 |
| 2 |
而t∈[
| 7 |
| 16 |
| 1 |
| 2 |
| 169 |
| 32 |
∴|
| TA |
| TB |
13
| ||
| 8 |
点评:本题考查轨迹方程,考查向量知识的运用,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
设双曲线C:
-y2=1的左、右顶点分别为A1、A2,垂直于x轴的直线l与双曲线C交于不同的两点P、Q.若直线l与x轴正半轴的交点为M,且
•
=1,则点M的坐标为( )
| x2 |
| 2 |
| A1P |
| A2Q |
A、(
| ||
| B、(2,0) | ||
C、(
| ||
| D、(3,0) |