题目内容
已知向量 =(
=( sin
sin ,1),
,1), =(cos
=(cos ,cos2
,cos2 ).记f(x)=
).记f(x)=
(1)求函数f(x)的最小正周期及单调递增区间;
(2)求当x∈(0,π)时,函数f(x)的值域.
解:(1)f(x)=
= sin
sin cos
cos +cos2
+cos2
= sin
sin +
+
 cos
cos
=sin( +
+ )
) .
.
最小正周期为T=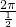 =4π.
=4π.
由2kπ- ≤
≤ +
+ ≤2kπ+
≤2kπ+ ,(k∈Z).
,(k∈Z).
∴4kπ- ≤x≤4kπ+
≤x≤4kπ+ ,
,
函数递增区间为[4kπ- ,4kπ+
,4kπ+ ](k∈Z).
](k∈Z).
(2)x∈(0,π),∴ +
+ ∈(
∈( ),
),
∴ <sin(
<sin( +
+ )≤1,
)≤1,
∴fmax∈(1, ].
].
分析:(1)由向量 =(
=( sin
sin ,1),
,1), =(cos
=(cos ,cos2
,cos2 ).f(x)=
).f(x)= 根据平面向量的数量积公式,结合降幂公式(二倍角公式逆用)及辅助角公式,将函数的解析式化为正弦型函数的形式,进而根据正弦型函数的性质,即可求出函数的周期,求出函数f(x)的单调递增区间;
根据平面向量的数量积公式,结合降幂公式(二倍角公式逆用)及辅助角公式,将函数的解析式化为正弦型函数的形式,进而根据正弦型函数的性质,即可求出函数的周期,求出函数f(x)的单调递增区间;
(2)由(1)中函数的解析式,结合x的范围,求出相位的范围,直接求解函数的最值.
点评:本题考查的知识点是平面向量的数量积运算,正弦型函数的图象和性质,根据平面向量的数量积公式和辅助角公式,求出函数的解析式是解答本题的关键.

=
 sin
sin cos
cos +cos2
+cos2
=
 sin
sin +
+
 cos
cos
=sin(
 +
+ )
) .
.最小正周期为T=
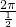 =4π.
=4π.由2kπ-
 ≤
≤ +
+ ≤2kπ+
≤2kπ+ ,(k∈Z).
,(k∈Z). ∴4kπ-
 ≤x≤4kπ+
≤x≤4kπ+ ,
,函数递增区间为[4kπ-
 ,4kπ+
,4kπ+ ](k∈Z).
](k∈Z).(2)x∈(0,π),∴
 +
+ ∈(
∈( ),
),∴
 <sin(
<sin( +
+ )≤1,
)≤1,∴fmax∈(1,
 ].
].分析:(1)由向量
 =(
=( sin
sin ,1),
,1), =(cos
=(cos ,cos2
,cos2 ).f(x)=
).f(x)= 根据平面向量的数量积公式,结合降幂公式(二倍角公式逆用)及辅助角公式,将函数的解析式化为正弦型函数的形式,进而根据正弦型函数的性质,即可求出函数的周期,求出函数f(x)的单调递增区间;
根据平面向量的数量积公式,结合降幂公式(二倍角公式逆用)及辅助角公式,将函数的解析式化为正弦型函数的形式,进而根据正弦型函数的性质,即可求出函数的周期,求出函数f(x)的单调递增区间;(2)由(1)中函数的解析式,结合x的范围,求出相位的范围,直接求解函数的最值.
点评:本题考查的知识点是平面向量的数量积运算,正弦型函数的图象和性质,根据平面向量的数量积公式和辅助角公式,求出函数的解析式是解答本题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目