题目内容
【题目】某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按![]() 元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
元/次收费, 并注册成为会员, 对会员逐次消费给予相应优惠,标准如下:
消费次第 | 第 | 第 | 第 | 第 |
|
收费比例 |
|
|
|
|
|
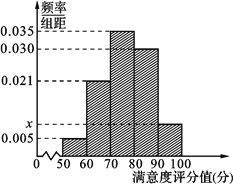
该公司从注册的会员中, 随机抽取了![]() 位进行统计, 得到统计数据如下:
位进行统计, 得到统计数据如下:
消费次第 | 第 | 第 | 第 | 第 | 第 |
频数 |
|
|
|
|
|
假设汽车美容一次, 公司成本为![]() 元, 根据所给数据, 解答下列问题:
元, 根据所给数据, 解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次, 求这两次消费中, 公司获得的平均利润;
(3)设该公司从至少消费两次, 求这的顾客消费次数用分层抽样方法抽出![]() 人, 再从这
人, 再从这![]() 人中抽出
人中抽出![]() 人发放纪念品, 求抽出
人发放纪念品, 求抽出![]() 人中恰有
人中恰有![]() 人消费两次的概率.
人消费两次的概率.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)直接根据古典概型概率公式求解即可;(2)先求出该会员第一次消费、第二 次消费公司获得的利润,然后求平均值即可;(3)先根据分层抽样的原理算出抽出的![]() 人中, 消费
人中, 消费![]() 次的有
次的有![]() 人,随机抽两人,共有
人,随机抽两人,共有![]() 种抽法,抽出
种抽法,抽出![]() 人中恰有
人中恰有![]() 人消费两次共有
人消费两次共有![]() 种,再根据古典概型概率公式可得结果.
种,再根据古典概型概率公式可得结果.
试题解析:(1)![]() 位会员中, 至少消费两次的会员有
位会员中, 至少消费两次的会员有![]() 人, 所以估计一位会员至少消费两次的概率为
人, 所以估计一位会员至少消费两次的概率为![]() .
.
(2)该会员第![]() 次消费时, 公司获得利润为
次消费时, 公司获得利润为![]() (元), 第
(元), 第![]() 次消费时, 公司获得利润为
次消费时, 公司获得利润为![]() (元), 所以, 公司这两次服务的平均利润为
(元), 所以, 公司这两次服务的平均利润为![]() (元).
(元).
(3)至少消费两次的会员中, 消费次数分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的比例为
的比例为![]() ,所以
,所以
抽出的![]() 人中, 消费
人中, 消费![]() 次的有
次的有![]() 人, 设为
人, 设为![]() ,消费
,消费![]() 次的有
次的有![]() 人, 设为
人, 设为![]() ,消费
,消费![]() 次和
次和![]() 次的各有
次的各有![]() 人, 分别设为
人, 分别设为![]() ,从中取
,从中取![]() 人, 取到
人, 取到![]() 的有:
的有:![]() 共
共![]() 种;
种;
去掉![]() 后, 取到
后, 取到![]() 的有:
的有:![]() 共
共![]() 种;
种;
去掉![]() 后, 取到
后, 取到![]() 的有:
的有:![]() 共
共![]() 种, 总的取法有
种, 总的取法有![]() 种,
种,
其中恰有![]() 人消费两次的取法共有:
人消费两次的取法共有:![]() 种,
种,
所以, 抽出![]() 人中恰有
人中恰有![]() 人费两次的概率为
人费两次的概率为![]() .
.

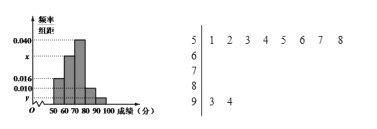
【题目】2016年巴西奥运会的周边商品有80%左右为“中国制造”,所有的厂家都是经过层层筛选才能获此殊荣.甲、乙两厂生产同一产品,为了解甲、乙两厂的产品质量,以确定这一产品最终的供货商,采用分层抽样的方法从甲、乙两厂生产的产品共98件中分别抽取9件和5件,测量产品中的微量元素的含量(单位:毫克).下表是从乙厂抽取的5件产品的测量数据:
编号 | 1 | 2 | 3 | 4 | 5 |
| 169 | 178 | 166 | 175 | 180 |
| 75 | 80 | 77 | 70 | 81 |
(1)求乙厂生产的产品数量:
(2)当产品中的微量元素![]() 满足:
满足:![]() ,且
,且![]() 时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量:
时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量:
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数的分布列及数学期望.