Question

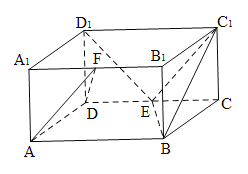
【题目】如图，四边形是边长为2的菱形，平面，为的中点．

（1）求证：平面平面；

（2）若，求三棱锥的体积．

Answer 1

【答案】（1）详见解析（2）1

【解析】

试题分析：（1）证明面面垂直，一般利用面面垂直判定定理，即从线面垂直出发给予证明，而题中已知线面垂直平面，因此可借助平行进行转化论证，这往往需利用平几知识，如本题利用三角形中位线性质，即得平面（2）求三棱锥体积，关键在于确定高，而高的寻找往往利用线面垂直平面，利用分割法得三棱锥的体积，转化的三个锥的高分别为,最后代入体积公式可得结果

试题解析：

（1）证明：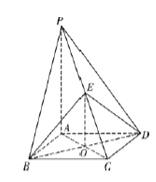

如图， 连接交于点，连接，

∵四边形是菱形，

∴，

∵为中点，

∴，

∵平面，∴平面，

∵平面，

∴平面平面．．．．．．．．．．．．．．．．．6分

（2）解：∵四边形是边长为2的菱形，

∴，

∵平面，

∴，∴，

∵，∴，∴，．．．．．．．．．．．．．．．．．．．．．．．． 9分

．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分