题目内容
(2012•开封一模)已知函数f(x)=
.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设函数g(x)=xf(x)+tf'(x)+e-x(t∈R).是否存在实数a、b、c∈[0,1],使得g(a)+g(b)<g(c)?若存在,求实数t的取值范围;若不存在,请说明理由.
| x+1 | ex |
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)设函数g(x)=xf(x)+tf'(x)+e-x(t∈R).是否存在实数a、b、c∈[0,1],使得g(a)+g(b)<g(c)?若存在,求实数t的取值范围;若不存在,请说明理由.
分析:(Ⅰ)求导函数,利用导数小于(等于)0,求得函数的单调减区间;利用导数大于(等于)0,求得函数的单调增区间;
(Ⅱ)假设存在a,b,c∈[0,1]使得g(a)+g(b)<g(c),则问题转化为2[g(x)]min<[g(x)]max,对t进行讨论,确定函数的单调性,从而确定函数的最值,进而确定实数t的取值范围.
(Ⅱ)假设存在a,b,c∈[0,1]使得g(a)+g(b)<g(c),则问题转化为2[g(x)]min<[g(x)]max,对t进行讨论,确定函数的单调性,从而确定函数的最值,进而确定实数t的取值范围.
解答:解:(Ⅰ)f/(x)=
当x≥0时,f/(x)=
≤0,函数在区间(0,+∞)上为减函数;当x<0时,f/(x)=
> 0,函数在区间(-∞,0)上为增函数
(Ⅱ)假设存在a,b,c∈[0,1]使得g(a)+g(b)<g(c),2[g(x)]min<[g(x)]max
∵g(x)=
,∴g/(x)=
①当t≥1时,g′(x)≤0,g(x)在[0,1]上单调递减,∴2g(1)<g(0)即2•
<1得t>3-
>1
②当t≤0时,g′(x)≥0,g(x)在[0,1]上单调递增,∴2g(0)<g(1)即2<
得t<3-2e<0,
③当0<t<1时,在x∈[0,t),
g′(x)<0,g(x)在[0,t]上单调递减,
在x∈(t,1],g′(x)>0,g(x)在[t,1]上单调递增,
此时g(x)的最小值为g(t),最大值为max{g(0),g(1)},
∴2g(t)<max{g(0),g(1)},即2×
<•max{1,
}(★) …(13分)
由(1)知f(t)=
在t∈[0,1]上单调递减,故2×
≥
,而
≤
,∴不等式(★)无解 …(15分)
综上所述,存在t∈(-∞,3-2e)∪(3-
,+∞),使得命题成立.
| -x |
| ex |
当x≥0时,f/(x)=
| -x |
| ex |
| -x |
| ex |
(Ⅱ)假设存在a,b,c∈[0,1]使得g(a)+g(b)<g(c),2[g(x)]min<[g(x)]max
∵g(x)=
| x2+(1-t)x+1 |
| ex |
| -(x-t)(x-1) |
| ex |
①当t≥1时,g′(x)≤0,g(x)在[0,1]上单调递减,∴2g(1)<g(0)即2•
| 3-t |
| e |
| e |
| 2 |
②当t≤0时,g′(x)≥0,g(x)在[0,1]上单调递增,∴2g(0)<g(1)即2<
| 3-t |
| e |
③当0<t<1时,在x∈[0,t),
g′(x)<0,g(x)在[0,t]上单调递减,
在x∈(t,1],g′(x)>0,g(x)在[t,1]上单调递增,
此时g(x)的最小值为g(t),最大值为max{g(0),g(1)},
∴2g(t)<max{g(0),g(1)},即2×
| t+1 |
| et |
| 3-t |
| e |
由(1)知f(t)=
| t+1 |
| et |
| t+1 |
| et |
| 4 |
| e |
| 3-t |
| e |
| 3 |
| e |
综上所述,存在t∈(-∞,3-2e)∪(3-
| e |
| 2 |
点评:本题主要考查利用导数求函数的单调区间,求函数的最值,注意分类讨论思想的运用,属于中档题.

练习册系列答案
相关题目
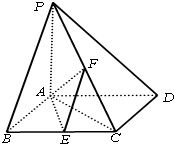 (2012•开封一模)已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
(2012•开封一模)已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.