题目内容
(08年长沙市模拟文)(13分) 已知函数f(x)=ax3+bx2-3x在![]() 处取得极值。
处取得极值。
(1)求函数f(x)的解析式;
(2)求证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有![]() ;
;
(3)若过点A(1,m)(m?-2)可作曲线y=f(x)的三条切线,求实数m的取值范围。
解析:(1)![]() ,依题意,
,依题意,![]() ,
,
即![]() ,解得
,解得![]() 3分
3分
(2)![]()
当-1<x<1时,![]() ,故f(x)在区间[-1,1]上为减函数,
,故f(x)在区间[-1,1]上为减函数,
![]()
∵对于区间[-1,1]上任意两个自变量的值x1,x2,
都有![]()
![]() 7分
7分
(3)![]() ,
,
∵曲线方程为y=x3-3x,∴点A(1,m)不在曲线上,
设切点为M(x0,y0),则点M的坐标满足![]() 。
。
因![]() ,故切线的斜率为
,故切线的斜率为![]() ,
,
整理得![]() 。
。
∵过点A(1,m)可作曲线的三条切线,
∴关于x0方程![]() 有三个实根。 9分
有三个实根。 9分
设![]() ,则
,则![]() ,
,
由![]() ,得x0=0或x0=1。
,得x0=0或x0=1。
![]() 在
在![]() 上单调递增,在(0,1)上单调递减。
上单调递增,在(0,1)上单调递减。
∴函数![]() 的极值点为x0=0,x0=1
的极值点为x0=0,x0=1
∴关于x0方程![]() 有三个实根的充要条件是
有三个实根的充要条件是
![]() ,解得-3<m<-2。
,解得-3<m<-2。
故所求的实数a的取值范围是-3<m<-2。……13分

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
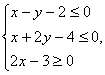 则
则