题目内容
已知函数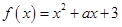 .
.
(Ⅰ)当 时,
时,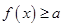 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅱ)若对一切 ,
,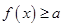 恒成立,求实数
恒成立,求实数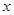 的取值范围.
的取值范围.
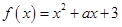 .
.(Ⅰ)当
 时,
时,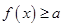 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(Ⅱ)若对一切
 ,
,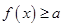 恒成立,求实数
恒成立,求实数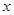 的取值范围.
的取值范围.(1) (2)
(2)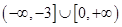
 (2)
(2)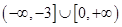
试题分析:(1)本题为含参二次函数求最值,涉及到的问题是轴动而区间不动,所以要分三种情况,对称轴在区间的左侧,在区间的右侧,在区间之间 .分别求出函数的最值从而解出a的取值范围.(2)与(1)的区别是给定了a的范围,解不等式,所以我们把
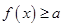 转化成关于a的不等式,利用给定a的范围恒成立问题来解决x的取值范围.
转化成关于a的不等式,利用给定a的范围恒成立问题来解决x的取值范围.试题解析:(Ⅰ)当
 时,设
时,设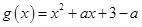 ,分以下三种情况讨论:
,分以下三种情况讨论:(1)当
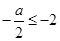 时,即
时,即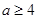 时,
时, 在
在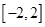 上单调递增,
上单调递增, ,
,因此
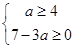 ,
, 无解.
无解.(2)当
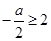 时,即
时,即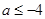 时,
时, 在
在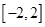 上单调递减,
上单调递减, ,
,因此
 ,解得
,解得 .
.(3)当
 时,即
时,即 时,
时, 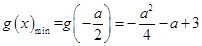 ,
,因此
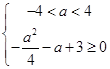 ,解得
,解得 .
.综上所述,实数
 的取值范围是
的取值范围是 . 6分
. 6分(Ⅱ) 由
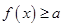 得
得 ,令
,令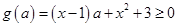 ,
,要使
 在区间
在区间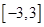 恒成立,只需
恒成立,只需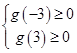 即
即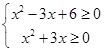 ,
,解得
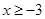 或
或 .所以实数
.所以实数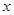 的取值范围是
的取值范围是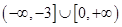 . 12分
. 12分
练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
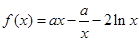
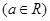
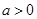 时,求
时,求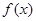 的单调区间;
的单调区间;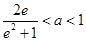 ,设
,设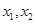 是函数
是函数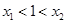 ,记
,记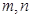 分别为
分别为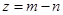 ,求实数
,求实数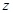 的取值范围.
的取值范围. 。
。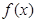 在
在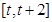
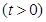 上的最小值;
上的最小值;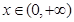 ,
,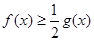 恒成立,求实数
恒成立,求实数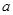 的取值范围.
的取值范围. 的零点所在的大致区间是( )
的零点所在的大致区间是( ) 其中
其中 ,曲线
,曲线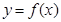 在点
在点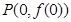 处的切线方程为
处的切线方程为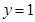 .
.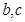 的值;
的值;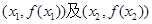 处的切线都过点(0,2).证明:当
处的切线都过点(0,2).证明:当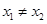 时,
时,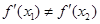 ;
;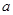 的取值范围.
的取值范围.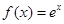 ,
,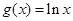 .
.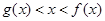 ;
;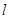 与
与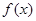 、
、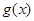 均相切,切点分别为(
均相切,切点分别为(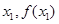 )、(
)、(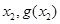 ),且
),且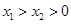 ,求证:
,求证: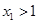 .
.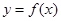 的图象在点
的图象在点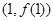 处的切线方程为
处的切线方程为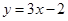 ,则函数
,则函数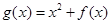 的图象在点
的图象在点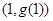 处的切线方程为 .
处的切线方程为 .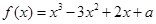 ,若
,若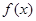 在
在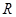 上的极值点分别为
上的极值点分别为 ,则
,则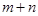 的值为( )
的值为( )