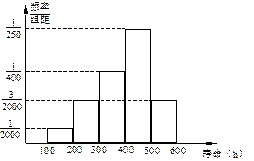题目内容
为了检验“喜欢玩手机游戏与认为作业多”是否有关系,某班主任对班级的30名学生进行了调查,得到一个2×2列联表:
| | 认为作业多 | 认为作业不多 | 合计 |
| 喜欢玩手机游戏 | 18 | 2 | |
| 不喜欢玩手机游戏 | | 6 | |
| 合计 | | | 30 |
(Ⅰ)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程);
(Ⅱ)能否在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系?
(Ⅲ)若从不喜欢玩手机游戏的人中随机抽取3人,则至少2人认为作业不多的概率是多少?
(Ⅰ) 认为作业多 认为作业不多 合计 喜欢玩手机游戏 18 2 20 不喜欢玩手机游戏 4 6 10 合计 22 8 30
(Ⅱ)在犯错误的概率不超过0.005的前提下,认为“喜欢玩手机游戏”与“认为作业多”有关.
(Ⅲ)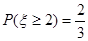 .
.
解析试题分析:(Ⅰ)根据所给数据,画出列联表;(Ⅱ)根据公式,求出这组数据的观测值,把观测值同临界值进行比较,即可得到结论;(Ⅲ)认为作业不多的人数为ξ,则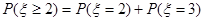 .
.
试题解析:(Ⅰ) 认为作业多 认为作业不多 合计 喜欢玩手机游戏 18 2 20 不喜欢玩手机游戏 4 6 10 合计 22 8 30
(Ⅱ)假设“喜欢玩手机游戏”与“认为作业多”无关.
则由上表数据得: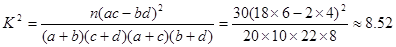 ,
,
又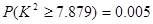 ,有8.52>7.879.
,有8.52>7.879.
故在犯错误的概率不超过0.005的前提下,认为“喜欢玩手机游戏”与“认为作业多”有关.
(Ⅲ)设认为作业不多的人数为ξ,则所求的概率为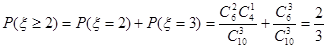 .
.
考点:独立性检验的应用;古典概型及其概率计算公式.

练习册系列答案
相关题目
某企业职工的月工资数统计如下:
| 月工资数(元) | 10000 | 8000 | 5500 | 2500 | 1600 | 1200 | 900 | 600 | 500 |
| 得此工资人数 | 1 | 3 | 3 | 8 | 20 | 35 | 45 | 3 | 2 |
请你站在其中一立场说明理由: 。
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | 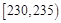 | 8 | 0.16 |
| 第二组 | 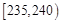 | ① | 0.24 |
| 第三组 | 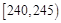 | 15 | ② |
| 第四组 | 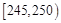 | 10 | 0.20 |
| 第五组 | 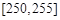 | 5 | 0.10 |
| 合 计 | 50 | 1.00 | |
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
某公司销售A、B、C三款手机,每款手机都有经济型和豪华型两种型号,据统计12月份共销售1000部手机(具体销售情况见下表)
| | A款手机 | B款手机 | C款手机 |
| 经济型 | 200 | x | y |
| 豪华型 | 150 | 160 | z |
已知在销售1000部手机中,经济型B款手机销售的频率是0.21.
(1)现用分层抽样的方法在A、B、C三款手机中抽取50部,求应在C款手机中抽取多少部?
(2)若y
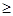 136,z
136,z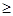 133,求C款手机中经济型比豪华型多的概率.
133,求C款手机中经济型比豪华型多的概率. 


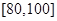 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份的分数在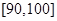 之间的概率;
之间的概率;

 的值;
的值; 与
与 中的学生人数;
中的学生人数; 的学生中人选2人,求此2人的成绩都在
的学生中人选2人,求此2人的成绩都在