题目内容
【题目】已知椭圆![]() :
:![]() 的两个焦点分别是
的两个焦点分别是![]() ,直线
,直线![]() :
:![]() 与椭圆交于
与椭圆交于![]() 两点.
两点.
(1)若![]() 为椭圆短轴上的一个顶点,且
为椭圆短轴上的一个顶点,且![]() 是直角三角形,求
是直角三角形,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,求证:
,求证:![]() 的面积为定值.
的面积为定值.
【答案】(1)![]() 或
或![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据![]() 为等腰直角三角形可知
为等腰直角三角形可知![]() ;分别讨论焦点在
;分别讨论焦点在![]() 轴和
轴和![]() 轴上的两种情况,构造方程求得
轴上的两种情况,构造方程求得![]() ;
;
(2)根据![]() 可知
可知![]() ,将直线
,将直线![]() 方程与椭圆
方程与椭圆![]() 方程联立,得到韦达定理的形式,代入
方程联立,得到韦达定理的形式,代入![]() 可整理得到
可整理得到![]() 的关系;利用弦长公式和点到直线距离公式可表示出
的关系;利用弦长公式和点到直线距离公式可表示出![]() 的面积,化简整理可得定值.
的面积,化简整理可得定值.
(1)![]() 为椭圆短轴上的一个顶点,且
为椭圆短轴上的一个顶点,且![]() 是直角三角形,
是直角三角形,
![]()
![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
当![]() 时,
时,![]() ,解得:
,解得:![]() ;
;
当![]() 时,
时,![]() ,解得:
,解得:![]() ;
;
![]()
![]() 或
或![]() .
.
(2)证明:当![]() 时,椭圆方程为:
时,椭圆方程为:![]() ,
,
设![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,
由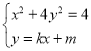 整理得:
整理得:![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,
![]()
![]()
![]() ,
,![]() ,满足
,满足![]() ,
,
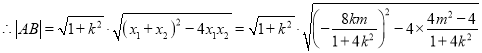
![]()
![]() .
.
![]() 到直线
到直线![]() 的距离为
的距离为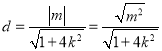 ,
,
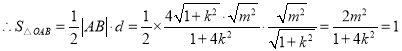 ,
,
![]() 的面积为定值
的面积为定值![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】某种水果按照果径大小可分为四类:标准果,优质果,精品果,礼品果.某采购商从采购的一批水果中随机抽取100个,利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)用样本估计总体,果园老板提出两种购销方案给采购商参考:
方案1:不分类卖出,单价为20元/![]() .
.
方案2:分类卖出,分类后的水果售价如下表:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/ | 16 | 18 | 22 | 24 |
从采购商的角度考虑,应该采用哪种方案较好?并说明理由.
(2)从这100个水果中用分层抽样的方法抽取10个,再从抽取的10个水果中随机抽取3个,![]() 表示抽取到精品果的数量,求
表示抽取到精品果的数量,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.