Question

15．如图，在四棱锥P-ABCD中，PA丄平面ABCD，AC丄AD，AB丄BC，∠BCA=45°，AP=AD=AC=2．
（Ⅰ）证明PC丄AD；
（Ⅱ）求二面角A-PC-D的余弦值；
（Ⅲ）棱PA上是否存在点E，使得平面PCD丄平面BCE，若存在，试确定点E的位置，若不存在，请说明理由．

Answer 1

分析 （Ⅰ）以点A为原点建立空间直角坐标系，确定$\overrightarrow{PC}$=（0，1，-2），$\overrightarrow{AD}$=（2，0，0），利用数量积公式，即可证明证明PC丄AD；
（Ⅱ）求平面PCD的一个法向量、平面PAC的一个法向量，利用向量的夹角公式求二面角A-PC-D的余弦值；
（Ⅲ）设点E的坐标为（0，0，a），其中0≤a≤2，求出平面EBC的法向量，利用平面PDC丄平面BCE，则$\overrightarrow n⊥\overrightarrow u$，即可得出结论．

解答 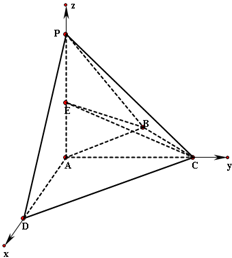解：如图，以点A为原点建立空间直角坐标系，依题意得
A（0，0，0），D（2，0，0），C（0，2，0），B（-1，1，0），P（0，0，2），…2分
（I）$\overrightarrow{PC}$=（0，1，-2），$\overrightarrow{AD}$=（2，0，0）
于是$\overrightarrow{PC}•\overrightarrow{AD}$=0，所以PC⊥AD．…4分
（II）$\overrightarrow{PC}=（0，2，-2）$，$\overrightarrow{CD}=（2，-2，0）$，设平面PCD的一个法向量$\overrightarrow n$=（（x，y，z）
则$\left\{\begin{array}{l}n•\overrightarrow{PC}=0\\ n•\overrightarrow{CD}=0\end{array}\right.$，即$\left\{\begin{array}{l}2y-2z=0\\ 2x-2y=0\end{array}\right.$，
不妨令z=1，可得$\overrightarrow n=（1，1，1）$…6分
取平面PAC的一个法向量$\overrightarrow m=（1，0，0）$，
于是$cos\left?{\overrightarrow m，\overrightarrow n}\right＞=\frac{\overrightarrow m•\overrightarrow n}{{|{\overrightarrow m}|•|{\overrightarrow n}|}}=\frac{{\sqrt{3}}}{3}$，所以二面角A-PC-D的余弦值为$\frac{{\sqrt{3}}}{3}$．…8分
（III）设点E的坐标为（0，0，a），其中0≤a≤2，…9分
又B（-1，1，0），故$\overrightarrow{EB}=（-1，1，-a）$
又$\overrightarrow{BC}=（1，1，0）$，设平面EBC的法向量为$\overrightarrow u=（x，y，z）$
则$\left\{\begin{array}{l}x+y=0\\-x+y-az=0\end{array}\right.$，取$\overrightarrow u=（-a，a，2）$…11分
若平面PDC丄平面BCE，则$\overrightarrow n⊥\overrightarrow u$，即$\overrightarrow n•\overrightarrow u=-a+a+2=0$，
满足条件的a值不存在，故没有满足条件的点E…13分．

点评 本题考查直线与直线，平面与平面垂直，考查二面角A-PC-D的余弦值，正确建立坐标系，求出平面的法向量是关键．