题目内容
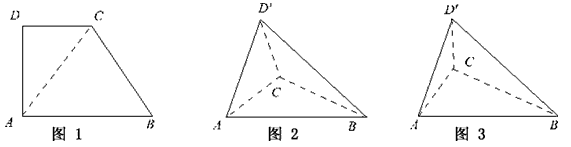
在直角梯形ABCD中,∠D=∠BAD=90°,AD=DC=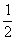 AB=a(如图1)。将△ADC沿AC折起,使D到D′。记面ACD′为α,面ABC为β,面BCD′为γ,
AB=a(如图1)。将△ADC沿AC折起,使D到D′。记面ACD′为α,面ABC为β,面BCD′为γ,
(Ⅰ)若二面角α-AC-β为直二面角(如图2),求二面角β-BC-γ的大小;
(Ⅱ)若二面角α-AC-β为60°(如图3),求三棱锥D′-ABC的体积。
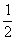 AB=a(如图1)。将△ADC沿AC折起,使D到D′。记面ACD′为α,面ABC为β,面BCD′为γ,
AB=a(如图1)。将△ADC沿AC折起,使D到D′。记面ACD′为α,面ABC为β,面BCD′为γ,(Ⅰ)若二面角α-AC-β为直二面角(如图2),求二面角β-BC-γ的大小;
(Ⅱ)若二面角α-AC-β为60°(如图3),求三棱锥D′-ABC的体积。
解:(Ⅰ)在直角梯形ABCD中,由已知△DAC为等腰直角三角形,
∴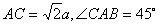 ,
,
过C作CH⊥AB,由AB=2a,可推得AC=BC=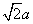 ,
,
∴AC⊥BC,
取AC的中点E,连结D′E,
则D′E⊥AC,
又∵二面角α-AC-β为直二面角,
∴D′E⊥β,
又∵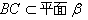 ,
,
∴BC⊥D′E,
∴BC⊥α,而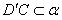 ,
,
∴BC⊥D′C,
∴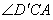 为二面角β-BC-γ的平面角。
为二面角β-BC-γ的平面角。
由于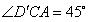 ,
,
∴二面角β-BC-γ为45°。
(Ⅱ)取AC的中点E,连结D′E,再过D′作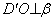 ,垂足为O,连结OE,
,垂足为O,连结OE,
∵AC⊥D′E,
∴AC⊥OE,
∴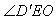 为二面角α-AC-β的平面角,
为二面角α-AC-β的平面角,
∴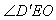 =60°,
=60°,
在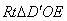 中,
中,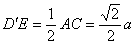 ,
,
∴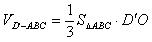
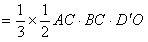
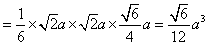 。
。
∴
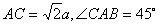 ,
,过C作CH⊥AB,由AB=2a,可推得AC=BC=
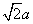 ,
, ∴AC⊥BC,
取AC的中点E,连结D′E,
则D′E⊥AC,
又∵二面角α-AC-β为直二面角,
∴D′E⊥β,
又∵
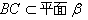 ,
,∴BC⊥D′E,
∴BC⊥α,而
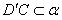 ,
,∴BC⊥D′C,
∴
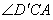 为二面角β-BC-γ的平面角。
为二面角β-BC-γ的平面角。由于
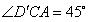 ,
,∴二面角β-BC-γ为45°。
(Ⅱ)取AC的中点E,连结D′E,再过D′作
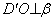 ,垂足为O,连结OE,
,垂足为O,连结OE, ∵AC⊥D′E,
∴AC⊥OE,
∴
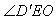 为二面角α-AC-β的平面角,
为二面角α-AC-β的平面角,∴
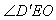 =60°,
=60°,在
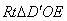 中,
中,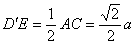 ,
, ∴
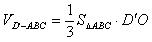
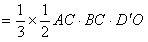
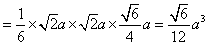 。
。 
练习册系列答案
相关题目
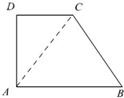
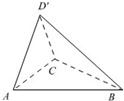
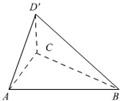
 (2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
(2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
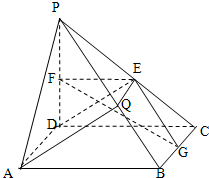
 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD= 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为