题目内容

设数列{an}的前n项和Sn=2n-1，则(+…+)等于(    )

A.                  B.1                  C.                 D.2

A

解析：当n=1时，a1=S1=2-1=1,当n≥2时，an=Sn-Sn-1=2n-1-2n-1+1=2n-1.此时n=1也成立，∴an=2n-1.

∴==()2n-1,它是以为首项、公比为的等比数列.

∴(+…+)=.

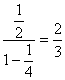练习册系列答案
相关题目
设数列{an}的前n项的和为Sn，且Sn=3n+1．
（1）求数列{an}的通项公式；
（2）设bn=an（2n-1），求数列{bn}的前n项的和．
设数列an的前n项的和为Sn，a1=
3
2
，Sn=2an+1-3．
（1）求a2，a3；
（2）求数列an的通项公式；
（3）设bn=(2log
3
2
an+1)•an，求数列bn的前n项的和Tn．
设数列{an}的前n项和Sn=2an+
3
2
×（-1）n-
1
2
，n∈N*．
（Ⅰ）求an和an-1的关系式；
（Ⅱ）求数列{an}的通项公式；
（Ⅲ）证明：
1
S1
+
1
S2
+…+
1
Sn
＜
10
9
，n∈N*．
不等式组
x≥0
y≥0
nx+y≤4n
所表示的平面区域为Dn，若Dn内的整点（整点即横坐标和纵坐标均为整数的点）个数为an（n∈N*）
（1）写出an+1与an的关系（只需给出结果，不需要过程），
（2）求数列{an}的通项公式；
（3）设数列an的前n项和为Sn且Tn=
Sn
5•2n
，若对一切的正整数n，总有Tn≤m成立，求m的范围．
（2013•郑州一模）设数列{an}的前n项和Sn=2n-1，则
S4
a3
的值为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网