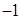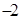题目内容
已知函数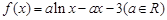 .(I)当
.(I)当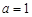 时,求函数
时,求函数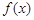 的单调区间;(II)若函数
的单调区间;(II)若函数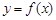 的图象在点
的图象在点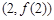 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的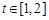 ,函数
,函数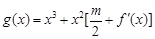 在区间
在区间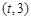 上总存在极值?
上总存在极值?
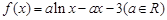 .(I)当
.(I)当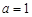 时,求函数
时,求函数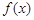 的单调区间;(II)若函数
的单调区间;(II)若函数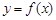 的图象在点
的图象在点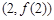 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的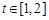 ,函数
,函数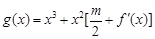 在区间
在区间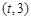 上总存在极值?
上总存在极值?(1)在(0,1)上单调递增;在(1,+∞)上单调递减. (2)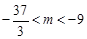
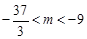
本试题主要考查了导数在研究函数中的运用。通过a的值可知,函数解析式,求解导数,然后令导数大于零和导数小于零,得到单调区间。并利用导数的几何意义得到切线的斜率等的运用。、
(1)直接求解导数,然后解导数的不等式得到单调增减区间。
(2)利用对于任意的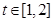 ,函数y=g(x)在区间
,函数y=g(x)在区间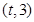 上总存在极值,转化为
上总存在极值,转化为
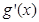 在x=2,x=3处的导数值分别为小于零和大于零得到参数m的取值范围。
在x=2,x=3处的导数值分别为小于零和大于零得到参数m的取值范围。
解: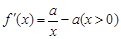
(I)当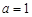 时,
时,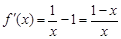 , …………………………………2分
, …………………………………2分
令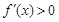 时,解得
时,解得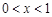 ,所以
,所以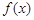 在(0,1)上单调递增; ……4分
在(0,1)上单调递增; ……4分
令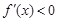 时,解得
时,解得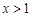 ,所以
,所以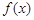 在(1,+∞)上单调递减. ………6分
在(1,+∞)上单调递减. ………6分
(II)因为函数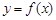 的图象在点(2,
的图象在点(2,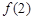 )处的切线的倾斜角为45o,
)处的切线的倾斜角为45o,
所以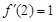 .
.
所以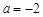 ,
,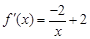 . ………………………………………………8分
. ………………………………………………8分
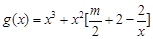
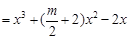 ,
,
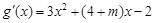 , ……………………………………………10分
, ……………………………………………10分
因为任意的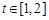 ,函数
,函数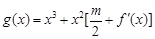 在区间
在区间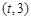 上总存在极值,
上总存在极值,
所以只需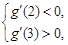 ……………………………………………………12分
……………………………………………………12分
解得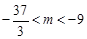 .
.
(1)直接求解导数,然后解导数的不等式得到单调增减区间。
(2)利用对于任意的
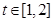 ,函数y=g(x)在区间
,函数y=g(x)在区间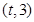 上总存在极值,转化为
上总存在极值,转化为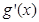 在x=2,x=3处的导数值分别为小于零和大于零得到参数m的取值范围。
在x=2,x=3处的导数值分别为小于零和大于零得到参数m的取值范围。解:
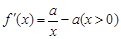
(I)当
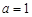 时,
时,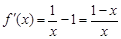 , …………………………………2分
, …………………………………2分令
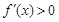 时,解得
时,解得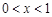 ,所以
,所以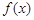 在(0,1)上单调递增; ……4分
在(0,1)上单调递增; ……4分令
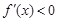 时,解得
时,解得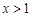 ,所以
,所以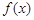 在(1,+∞)上单调递减. ………6分
在(1,+∞)上单调递减. ………6分(II)因为函数
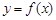 的图象在点(2,
的图象在点(2,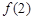 )处的切线的倾斜角为45o,
)处的切线的倾斜角为45o,所以
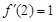 .
.所以
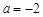 ,
,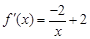 . ………………………………………………8分
. ………………………………………………8分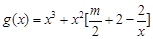
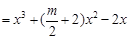 ,
,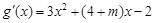 , ……………………………………………10分
, ……………………………………………10分因为任意的
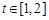 ,函数
,函数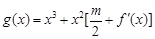 在区间
在区间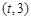 上总存在极值,
上总存在极值,所以只需
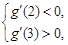 ……………………………………………………12分
……………………………………………………12分解得
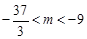 .
. 
练习册系列答案
相关题目
 .
.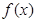 的单调区间;
的单调区间;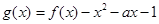 在区间
在区间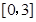 上的最小值.
上的最小值. 在
在 处导数
处导数 的几何意义是( )
的几何意义是( ) 轴所夹的锐角正切值;
轴所夹的锐角正切值; 在点 ( x0,f ( x0 ) ) 处的切线的斜率.
在点 ( x0,f ( x0 ) ) 处的切线的斜率.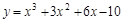 的切线中,斜率最小的的切线方程为
的切线中,斜率最小的的切线方程为 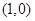 的直线与曲线
的直线与曲线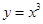 和
和 都相切,则
都相切,则
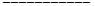
 (Ⅰ)当
(Ⅰ)当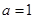 时,求曲线
时,求曲线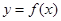 在点
在点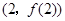 处的切线方程;
处的切线方程;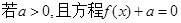 有三个不同的实数解,求
有三个不同的实数解,求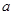 的取值范围.
的取值范围. ,f(1)=-1,则此函数为( )
,f(1)=-1,则此函数为( )

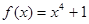

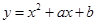 在点
在点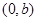 处的切线斜率为1,且切线方程是
处的切线斜率为1,且切线方程是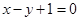 ,
,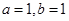
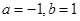
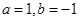
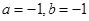
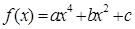 满足
满足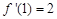 ,则
,则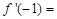 ( )
( )