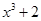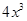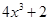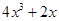题目内容
若存在过点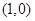 的直线与曲线
的直线与曲线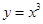 和
和 都相切,则
都相切,则
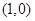 的直线与曲线
的直线与曲线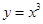 和
和 都相切,则
都相切,则
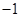 或
或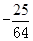
解:由y=x3⇒y'=3x2,设曲线y=x3上任意一点(x0,x03)处的切线方程为y- x03=3x02(x-x0),(1,0)代入方程得x0=0或x0="3" /2①当x0=0时,切线方程为y=0,则ax2+15 /4 x-9=0,△="(15/" 4 )2-4a×(-9)=0⇒a="-25/" 64
②当x0="3" 2 时,切线方程为y="27/" 4 x-27/ 4 ,由 y=ax2+15 /4 x-9 y="27" /4 x-27/ 4 ⇒ax2-3x-9 /4 =0,△="32-4a(-9/" 4 )=0⇒a=-1∴a="-25/" 64 或a=-1.
故答案为:-25 /64 或-1
②当x0="3" 2 时,切线方程为y="27/" 4 x-27/ 4 ,由 y=ax2+15 /4 x-9 y="27" /4 x-27/ 4 ⇒ax2-3x-9 /4 =0,△="32-4a(-9/" 4 )=0⇒a=-1∴a="-25/" 64 或a=-1.
故答案为:-25 /64 或-1

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
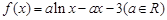 .(I)当
.(I)当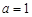 时,求函数
时,求函数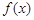 的单调区间;(II)若函数
的单调区间;(II)若函数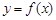 的图象在点
的图象在点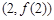 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的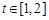 ,函数
,函数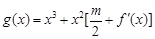 在区间
在区间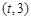 上总存在极值?
上总存在极值?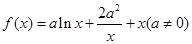 .
.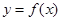 在点
在点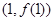 处的切线与直线
处的切线与直线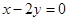 垂直,求实数
垂直,求实数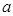 的值;
的值;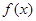 的单调性;
的单调性;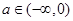 时,记函数
时,记函数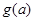 ,求证:
,求证: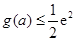 .
.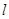 是曲线
是曲线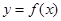 在
在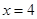 处的切线,则
处的切线,则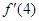 =
= 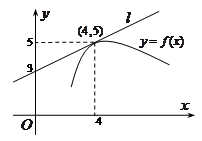
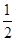
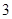
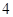
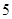
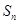 与n之间的关系如图所示,从目前记录的结果看,前m年的年平均产量最高,m的值为( )
与n之间的关系如图所示,从目前记录的结果看,前m年的年平均产量最高,m的值为( )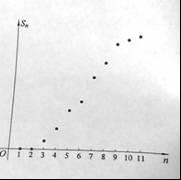
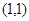 处的切线方程为________
处的切线方程为________ ,则
,则 ( )
( )



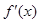 ,且满足f(x)= x3+2x
,且满足f(x)= x3+2x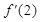 ,则
,则
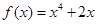 的导数
的导数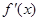 =( )
=( )