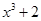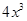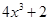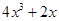题目内容
设函数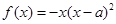 (Ⅰ)当
(Ⅰ)当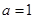 时,求曲线
时,求曲线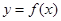 在点
在点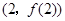 处的切线方程;
处的切线方程;
(Ⅱ)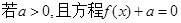 有三个不同的实数解,求
有三个不同的实数解,求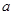 的取值范围.
的取值范围.
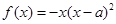 (Ⅰ)当
(Ⅰ)当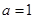 时,求曲线
时,求曲线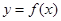 在点
在点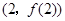 处的切线方程;
处的切线方程;(Ⅱ)
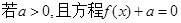 有三个不同的实数解,求
有三个不同的实数解,求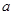 的取值范围.
的取值范围.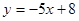 (2)
(2)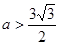 .
.本试题主要考查了函数与导数的综合运用。
第一问中,利用
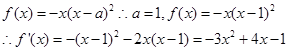
得到斜率和点的坐标,表示切线方程即可
第二问中,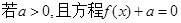 有三个不同的实数解
有三个不同的实数解
则利用函数g(x)=f(x)+a与x轴交点的个数来判定,求解导数,判定单调性和极值,然后利用极值与x轴的位置关系得到结论
解:因为
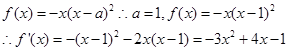
所以曲线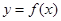 在点
在点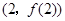 处的切线方程
处的切线方程
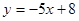 ……………………………………7分
……………………………………7分
(2)因为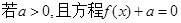 有三个不同的实数解则利用函数g(x)=f(x)+a与x轴交点的个数来判定,求解导数,判定单调性和极值,然后利用极值与x轴的位置关系得到结论。
有三个不同的实数解则利用函数g(x)=f(x)+a与x轴交点的个数来判定,求解导数,判定单调性和极值,然后利用极值与x轴的位置关系得到结论。
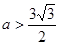 ……………………………………14分
……………………………………14分
第一问中,利用
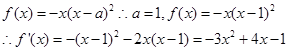
得到斜率和点的坐标,表示切线方程即可
第二问中,
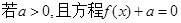 有三个不同的实数解
有三个不同的实数解则利用函数g(x)=f(x)+a与x轴交点的个数来判定,求解导数,判定单调性和极值,然后利用极值与x轴的位置关系得到结论
解:因为
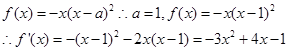
所以曲线
 在点
在点 处的切线方程
处的切线方程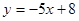 ……………………………………7分
……………………………………7分(2)因为
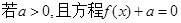 有三个不同的实数解则利用函数g(x)=f(x)+a与x轴交点的个数来判定,求解导数,判定单调性和极值,然后利用极值与x轴的位置关系得到结论。
有三个不同的实数解则利用函数g(x)=f(x)+a与x轴交点的个数来判定,求解导数,判定单调性和极值,然后利用极值与x轴的位置关系得到结论。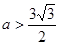 ……………………………………14分
……………………………………14分
练习册系列答案
相关题目
 .(I)当
.(I)当 时,求函数
时,求函数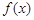 的单调区间;(II)若函数
的单调区间;(II)若函数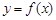 的图象在点
的图象在点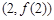 处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的
处的切线的倾斜角为45o,问:m在什么范围取值时,对于任意的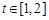 ,函数
,函数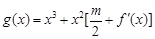 在区间
在区间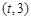 上总存在极值?
上总存在极值?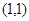 处的切线方程为________
处的切线方程为________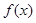 定义域为R,且
定义域为R,且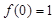 ,对任意
,对任意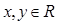 恒有
恒有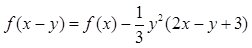 ,
,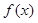 的表达式;
的表达式;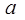 有三个实数解,求实数
有三个实数解,求实数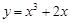 上一点(1,3)的切线方程是 .
上一点(1,3)的切线方程是 .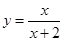 在点
在点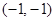 处的切线方程是( )
处的切线方程是( )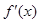 ,且满足f(x)= x3+2x
,且满足f(x)= x3+2x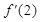 ,则
,则
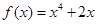 的导数
的导数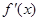 =( )
=( )