题目内容
已知函数f(x)=4x3-3x2cosθ+
,其中x∈R,θ为参数,且0≤θ≤2π.
①当cosθ=0时,判断函数f(x)是否有极值;
②要使函数f(x)的极小值小于零,求参数θ的取值范围;
③若对②中所求的取值范围内的任意参数θ,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
| 1 | 32 |
①当cosθ=0时,判断函数f(x)是否有极值;
②要使函数f(x)的极小值小于零,求参数θ的取值范围;
③若对②中所求的取值范围内的任意参数θ,函数f(x)在区间(2a-1,a)内都是增函数,求实数a的取值范围.
分析:①先求函数的导数,f′(x)>0在(-∞,+∞)上恒成立,得到函数的单调性,从而可判定是否有极值.
②先求出极值点,f′(x)=0的点附近的导数的符号的变化情况,来确定极值,求出极小值,使函数f(x)的极小值小于零建立不等关系,求出参数θ的取值范围即可.
③由②知,函数f(x)在区间(-∞,0)与 (
,+∞)内都是增函数,只需(2a-1,a)是区间(-∞,0)与 (
,+∞)的子集即可.
②先求出极值点,f′(x)=0的点附近的导数的符号的变化情况,来确定极值,求出极小值,使函数f(x)的极小值小于零建立不等关系,求出参数θ的取值范围即可.
③由②知,函数f(x)在区间(-∞,0)与 (
| cosθ |
| 2 |
| cosθ |
| 2 |
解答:解:①当cosθ=0时 f(x)=4x3+
,则f(x)在(-∞,+∞)内是增函数,
故无极值.
②f'(x)=12x2-6xcosθ,令f'(x)=0,
得 x1=0,x2=
.
由 0≤θ≤
及
<θ<2π,(只需考虑cosθ>0的情况).
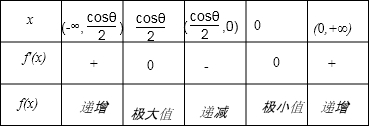
当x变化时,f'(x)的符号及f(x)的变化情况如下表:

因此,函数f(x)在 x=
处取得极小值 f(
),且 f(
)=-
cos3θ+
.
要使 f(
)<0,必有 -
cos3θ+
<0,
可得
<cosθ< 1,
所以 0<θ<
或
<θ<2π
当
<θ<
时,
当x变化时,f'(x)的符号及f(x)的变化情况如下表:
当x=0是,函数有极小值
,不满足题意.
所以 0<θ<
或
<θ<2π
③由②知,函数f(x)在区间(-∞,0)与 (
,+∞)内都是增函数.
由题设,函数f(x)在(2a-1,a)内是增函数,
则a须满足不等式组
或
由(II),0<θ<
或
<θ<2π时,
<cosθ< 1,
要使不等式 2a-1≥
cosθ关于参数θ恒成立,必有 2a-1≥
.
综上,解得a≤0或 a>1
所以a的取值范围是 (-∞,0]∪(1,+∞)
| 1 |
| 32 |
故无极值.
②f'(x)=12x2-6xcosθ,令f'(x)=0,
得 x1=0,x2=
| cosθ |
| 2 |
由 0≤θ≤
| π |
| 2 |
| 3π |
| 2 |
当x变化时,f'(x)的符号及f(x)的变化情况如下表:

因此,函数f(x)在 x=
| cosθ |
| 2 |
| cosθ |
| 2 |
| cosθ |
| 2 |
| 1 |
| 4 |
| 1 |
| 32 |
要使 f(
| cosθ |
| 2 |
| 1 |
| 4 |
| 1 |
| 32 |
可得
| 1 |
| 2 |
所以 0<θ<
| π |
| 3 |
| 5π |
| 3 |
当
| π |
| 2 |
| 3π |
| 2 |
当x变化时,f'(x)的符号及f(x)的变化情况如下表:

当x=0是,函数有极小值
| 1 |
| 32 |
所以 0<θ<
| π |
| 3 |
| 5π |
| 3 |
③由②知,函数f(x)在区间(-∞,0)与 (
| cosθ |
| 2 |
由题设,函数f(x)在(2a-1,a)内是增函数,
则a须满足不等式组
|
|
由(II),0<θ<
| π |
| 3 |
| 5π |
| 3 |
| 1 |
| 2 |
要使不等式 2a-1≥
| 1 |
| 2 |
| 1 |
| 2 |
综上,解得a≤0或 a>1
所以a的取值范围是 (-∞,0]∪(1,+∞)
点评:本小题主要考查运用导数研究函数的单调性及极值、解不等式等基础知识,考查综合分析和解决问题的能力.

练习册系列答案
相关题目